
设数列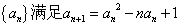 ,
,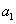 =2,n∈N*.
=2,n∈N*.
(Ⅰ)求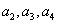 并由此猜想出
并由此猜想出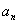 的一个通项公式;
的一个通项公式;
(Ⅱ)证明由(Ⅰ)猜想出的结论.
.解:(Ⅰ)由a1=2,得a2=a -a1+1=3,由a2=3,得a3=a
-a1+1=3,由a2=3,得a3=a -2a2+1=4,………… 3分
-2a2+1=4,………… 3分
由a3=4,得a4=a -3a3+1=5.由此猜想an的一个通项公式为:an=n+1(n∈N*).… 6分
-3a3+1=5.由此猜想an的一个通项公式为:an=n+1(n∈N*).… 6分
(Ⅱ)证明:①当n=1时,a1=2,猜想成立.………………………………………… 7分
②假设当n=k(k∈N*且k≥1)时猜想成立,即ak=k+1,
那么当n=k+1时,ak+1=ak(ak-k)+1=(k+1)(k+1-k)+1=k+2,……………… 11分
也就是说,当n=k+1时,ak+1=(k+1)+1. 猜想成立
根据①和②,对于所有n∈N*,都有an=n+1. ………………………………… 12分


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
设 是整数集
是整数集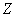 的非空子集,如果
的非空子集,如果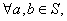 有
有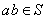 ,则称
,则称 关于数的乘法是封闭的. 若
关于数的乘法是封闭的. 若 ,
, 是
是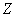 的两个不相交的非空子集,
的两个不相交的非空子集, 且
且 有
有 有
有 ,有四个命题:①
,有四个命题:① 中至少有一个关于乘法是封闭的;②
中至少有一个关于乘法是封闭的;② 中至多有一个关于乘法是封闭的;③
中至多有一个关于乘法是封闭的;③ 中有且只有一个关于乘法是封闭的; ④
中有且只有一个关于乘法是封闭的; ④ 中每一个关于乘法都是封闭的.其中所有正确命题的序号是 .
中每一个关于乘法都是封闭的.其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
在下列命题中:①若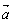 、
、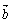 共线,则
共线,则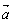 、
、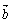 所在的直线平行; ②若
所在的直线平行; ②若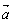 、
、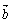 所在的直线是异面直线,则
所在的直线是异面直线,则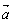 、
、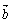 一定不共面; ③若
一定不共面; ③若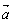 、
、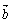 、
、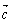 三向量两两共面,则
三向量两两共面,则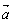 、
、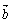 、
、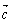 三向量一定也共面; ④已知三向量
三向量一定也共面; ④已知三向量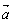 、
、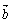 、
、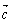 ,则空间任意一个向量
,则空间任意一个向量 总可以唯一表示为
总可以唯一表示为  .其中正确命题的个数为( )
.其中正确命题的个数为( )
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
过抛物线 y2 = 4x 的焦点作直线交抛物线于A(x1, y1)B(x2, y2)两点,如果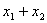 =6,
=6,
那么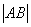 = ( )
= ( )
(A)6 (B)8 (C)9 (D)10
查看答案和解析>>
科目:高中数学 来源: 题型:
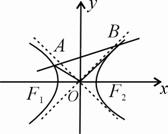
如图,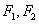 是双曲线
是双曲线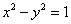 的两个焦点,O为坐标原点,圆
的两个焦点,O为坐标原点,圆 是以
是以 为直径的圆,直线
为直径的圆,直线 :
: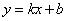 与圆O相切,并与双曲线交于A、B两点.
与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当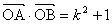 时,求直线
时,求直线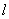 的方程;
的方程;
(Ⅲ)当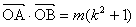 ,且满足
,且满足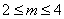 时,求
时,求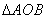 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com