
【题目】已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
【答案】(1)见解析.
(2)见解析.
(3) M={m|0<m<1}.
【解析】
(1)借助对称性作f(x)=|x2﹣4x+3|的图象即可,
(2)由图象写出函数f(x)的单调区间即可;
(3)作f(x)=|x2﹣4x+3|与y=m的图象,由二者的交点个数确定出集合M.
(1)当x2-4x+3≥0时,x≤1或x≥3,
∴f(x)=![]()
∴f(x)的图象为:
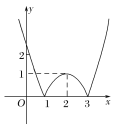
(2)由函数的图象可知f(x)的单调区间是(-∞,1],(2,3),(1,2],[3,+∞),其中(-∞,1],(2,3)是减区间;(1,2],[3,+∞)是增区间.
(3)由f(x)的图象知,当0<m<1时,f(x)=m有四个不相等的实根,所以M={m|0<m<1}.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A作直线m,与圆O相交于两点R,S,若△ORS是钝角三角形,求直线m的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.

(1)要使矩形AMPN的面积大于9平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为等差数列{an}的前n项和,S6=51,a5=13.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项公式是bn=![]() , 求数列{bn}的前n项和Sn .
, 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
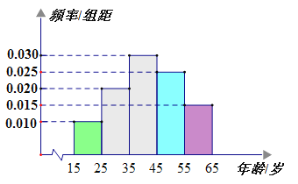
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,已知过点
,已知过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com