
【题目】设函数![]() ,则满足f(f(a))=2f(a)的a的取值范围是( )
,则满足f(f(a))=2f(a)的a的取值范围是( )
A. ![]() B. [0,1]
B. [0,1]
C. ![]() D. [1,+∞)
D. [1,+∞)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某种商品在![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (
(![]() )(天)的函数关系满足函数
)(天)的函数关系满足函数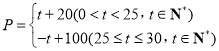 ,该商品在
,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (
(![]() )(天)之间满足一次函数关系如下表:
)(天)之间满足一次函数关系如下表:
第 |
|
|
|
|
|
|
|
|
|
(1)根据表中提供的数据,确定日销售量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(2)求该商品的日销售金额的最大值并指出日销售金额最大的一天是![]() 天中的第几天,(日销售金额
天中的第几天,(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的长轴长
的长轴长![]() ,短轴长
,短轴长![]() .
.

(1)求椭圆的方程;
(2)记椭圆的左右顶点![]() ,分别过
,分别过![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,
,![]() 为 椭圆上位于
为 椭圆上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.
(i)当直线![]() 的斜率为2时,求
的斜率为2时,求![]() 的面积;
的面积;
(ii)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},等比数列{bn}满足:a1=b1=1,a2=b2,2a3-b3=1.
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com