
对于函数f(x)若存在x0∈R,f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A,B两点的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+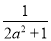 对称,求b的最小值.
对称,求b的最小值.
(1)-1和3.
(2)(0,1)
(3)-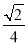
【解析】【解析】
(1)∵a=1,b=-2时,f(x)=x2-x-3,
f(x)=x⇒x2-2x-3=0⇒x=-1,x=3,
∴函数f(x)的不动点为-1和3.
(2)即f(x)=ax2+(b+1)x+b-1=x有两个不等实根,转化为ax2+bx+b-1=0有两个不等实根,需有判别式大于0恒成立,即Δ=b2-4a(b-1)>0⇒Δ1=(-4a)2-4×4a<0⇒0<a<1,
∴a的取值范围为(0,1).
(3)设A(x1,x1),B(x2,x2),则x1+x2=-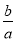 ,
,
则A,B中点M的坐标为(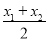 ,
,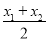 ),即M(-
),即M(-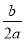 ,-
,-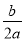 ).
).
∵A,B两点关于直线y=kx+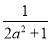 对称,
对称,
且A,B在直线y=x上,
∴k=-1,A,B的中点M在直线y=kx+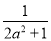 上.
上.
∴- =
=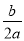 +
+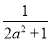 ⇒b=-
⇒b=- =-
=-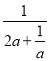 ,
,
利用基本不等式可得当且仅当a= 时,b的最小值为-
时,b的最小值为-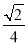 .
.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170-0.05x,试问生产多少件产品时,总利润最高?(总利润=总销售额-总成本)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-7函数的图象(解析版) 题型:选择题
已知函数f(x)的图象如图所示,则f(x)的解析式可以是( )
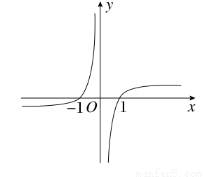
A.f(x)=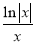
B.f(x)=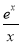
C.f(x)=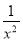 -1
-1
D.f(x)=x-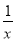
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-5指数及指数函数(解析版) 题型:填空题
如果函数f(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数,那么实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-4二次函数与幂函数(解析版) 题型:解答题
已知函数f(x)=xm-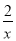 且f(4)=
且f(4)=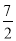 .
.
(1)求m的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-4二次函数与幂函数(解析版) 题型:选择题
若函数f(x)=x2-ax-a在区间[0,2]上的最大值为1,则实数a等于( )
A.-1 B.1 C.2 D.-2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-3函数的奇偶性与周期性(解析版) 题型:选择题
设定义在R上的函数f(x)满足f(x)·f(x+2)=13,若f(1)=2,则f(2015)=( )
A.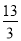 B.
B.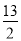 C.13 D.
C.13 D.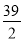
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:填空题
函数f(x)=-x3+mx2+1(m≠0)在(0,2)内的极大值为最大值,则m的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com