
函数f(x)=x+lnx的零点所在的区间为( )
A.(-1,0) B.( ,1) C.(1,2) D.(1,e)
,1) C.(1,2) D.(1,e)
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:填空题
定义一:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2 恒成立,则称函数f(x)在D内有一个宽度为d的.
定义二:若一个函数f(x),对于任意给定的正数?,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为?的,则称f(x)在正无穷处有.下列函数:
①f(x)=lgx,②f(x)=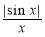 ,③f(x)=-
,③f(x)=-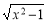 ,④f(x)=
,④f(x)=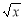 ,⑤f(x)=2x,⑥f(x)=3x-
,⑤f(x)=2x,⑥f(x)=3x-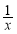
其中在正无穷处有的函数的序号是___________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:解答题
数列{an}的前n项和为Pn,若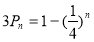 (n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(1)求数列{an}和{bn}的通项公式an和bn;
(2)设数列cn=anbn,求{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:填空题
已知函数f(x)是定义域为R的奇函数,且周期为2,若当x∈[0,1)时,f(x)=2x-1,则f(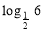 )的值是________________.
)的值是________________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
若(1+2ai)i=1-bi,其中a,b∈R,i是虚数单位,则|a+bi|=( )
A. +i B.
+i B.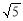 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:解答题
已知向量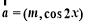 ,
,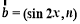 ,函数f(x)=
,函数f(x)=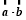 ,且y=f(x)的图象过点
,且y=f(x)的图象过点 和点
和点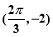 .
.
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:解答题
已知椭圆(a>b>0)和直线l:y=bx+2,椭圆的离心率e=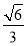 ,坐标原点到直线l的距离为
,坐标原点到直线l的距离为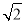 .
.
(1)求椭圆的方程;
(2)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆相交于C,D两点,试判断是否存在实数k,使得以CD为直径的圆过定点E?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com