
分析 由${a_n}{a_{n+1}}={3^n}$,得${a}_{n+1}{a}_{n+2}={3}^{n+1}$,两式作商得:$\frac{{a}_{n+2}}{{a}_{n}}=3$,由此可得数列{an}的奇数项和偶数项分别构成以3为公比的等比数列,分组后利用等比数列的前n项和求得S2015.
解答 解:由${a_n}{a_{n+1}}={3^n}$,得${a}_{n+1}{a}_{n+2}={3}^{n+1}$,
两式作商得:$\frac{{a}_{n+2}}{{a}_{n}}=3$,
又a1=1,∴a2=3,
则数列{an}的奇数项和偶数项分别构成以3为公比的等比数列,
∴S2015=(a1+a2+…+a2015)+(a2+a3+…+a2016)
=2[(a1+a3+…+a2015)+(a2+a4+…+a2014)]+a2016-a1
=2[$\frac{1×(1-{3}^{1008})}{1-3}+\frac{3×(1-{3}^{1007})}{1-3}$]+31003-1
=2×31008-4+31003-1
=2×31008+31003-5.
故答案为:2×31008+31003-5.
点评 本题考查数列递推式,考查了作商法求数列的通项公式,训练了数列的分组求和,考查等比数列的前n项和,是中档题.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中(如图),底面ABCD是直角梯形,M为PC中点,且AB∥DC,又∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
在四棱锥P-ABCD中(如图),底面ABCD是直角梯形,M为PC中点,且AB∥DC,又∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [25,30] | 3 | 0.12 |
| (30,35] | 5 | 0.20 |
| (35,40] | 8 | 0.32 |
| (40,45] | n1 | f1 |
| (45,50] | n2 | f2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
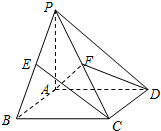 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | x1 | x2 | x3 |
| P | p1 | p2 | p3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com