练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

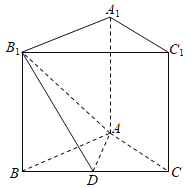
    【题目】如图，多面体ABCD﹣A1B1C1D1为正方体，则下面结论正确的是（　　）

    A.A1B∥B1C

    B.平面CB1D1⊥平面A1B1C1D1

    C.平面CB1D1∥平面A1BD

    D.异面直线AD与CB1所成的角为30°

    【答案】C

    【解析】

    根据正方体的顶点位置，可判断A1B、B1C是异面直线；平面CB1D1内不存在与平面A1B1C1D1

    垂直的直线，平面A1B1C1D1内不存在直线垂直平面CB1D1，平面CB1D1不垂直平面A1B1C1D1；根据面面平行的判断定理可证平面CB1D1∥平面A1BD；根据正方体边的平行关系，可得异面直线AD与CB1所成的角为45°，即可得出结论.

    选项A:平面平面平面，

    是异面直线，该选项不正确；

    选项B:由正方体可知，平面，

    平面，

    同理平面，

    而平面内不存在与平行的直线，

    所以平面内不存在直线垂直平面CB1D1；

    同理平面CB1D1内不存在垂直平面A1B1C1D1的直线，

    所以平面CB1D1不垂直平面A1B1C1D1，故该选项不正确；

    选项C：由正方体可得，可证平面，

    同理可证平面，根据面面平行的判断定理

    可得平面CB1D1∥平面A1BD，故该选项正确；

    选项D: ，异面直线AD与CB1所成的角为

    而，故该选项不正确.

    故选:C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中,且为常数）.

    (1)若对于任意的，都有成立，求的取值范围；

    (2)在(1)的条件下，若方程在上有且只有一个实根，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，当时，恒有．当时， ．

    （Ⅰ）求证： 是奇函数；

    （Ⅱ）若，试求在区间上的最值；

    （Ⅲ）是否存在，使对于任意恒成立？若存在，求出实数的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 设函数，其中.

    （Ⅰ）若，讨论的单调性；

    （Ⅱ）若，

    （i）证明恰有两个零点

    （ii）设为的极值点，为的零点，且，证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中（底面△ABC为正三角形），A1A⊥平面ABC，AB=AC=2，，D是BC边的中点．

    （1）证明：平面ADB1⊥平面BB1C1C．

    （2）求点B到平面ADB1的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝loga（x﹣1）（a＞0，且a≠1）．

    （1）若f（x）在[2，9]上的最大值与最小值之差为3，求a的值；

    （2）若a＞1，求不等式f（2x）＞0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （I）若，求在区间上的最大值和最小值；

    （II）解关于x的不等式

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）阅读下列材料并填空：对于二元一次方程组，我们可以将、的系数和相应的常数项排成一个数表，求得的一次方程组的解，用数表可表示为.用数表可以简化表达解一次方程组的过程如下，请补全其中的空白：，从而得到该方程组的解集________；

    （2）仿照（1）中数表的书写格式写出解方程组的过程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线经过点，其倾斜角为，在以原点为极点，轴非负半轴为极轴的极坐标系中（取相同的长度单位），曲线的极坐标方程为

    （Ⅰ）若直线与曲线有公共点，求的取值范围；

    （Ⅱ）设为曲线上任意一点，求的取值范围.

    查看答案和解析>>

    同步练习册答案