
已知函数f(x)=ax2-(a+2)x+ln x.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.
(1)y=-2.
(2)[1,+∞)
(3)[0,8]
【解析】(1)当a=1时,f(x)=x2-3x+ln x,f′(x)=2x-3+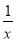 .
.
因为f′(1)=0,f(1)=-2.
所以切线方程是y=-2.
(2)函数f(x)=ax2-(a+2)x+ln x的定义域是(0,+∞).
当a>0时,f′(x)=2ax-(a+2)+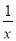 =
=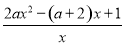 (x>0),
(x>0),
令f′(x)=0,即f′(x)=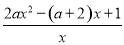
=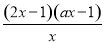 =0,
=0,
所以x=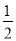 或x=
或x=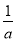 .
.
当0<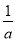 ≤1,即a≥1时,f(x)在[1,e]上单调递增,
≤1,即a≥1时,f(x)在[1,e]上单调递增,
所以f(x)在[1,e]上的最小值是f(1)=-2;
当1<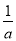 <e时,f(x)在[1,e]上的最小值是f
<e时,f(x)在[1,e]上的最小值是f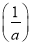 <f(1)=-2,不合题意;
<f(1)=-2,不合题意;
当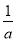 ≥e时,f(x)在(1,e)上单调递减,
≥e时,f(x)在(1,e)上单调递减,
所以f(x)在[1,e]上的最小值是f(e)<f(1)=-2,不合题意.
综上a的取值范围是[1,+∞).
(3)设g(x)=f(x)+2x,则g(x)=ax2-ax+ln x,
只要g(x)在(0,+∞)上单调递增即可.
而g′(x)=2ax-a+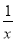 =
=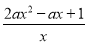 ,
,
当a=0时,g′(x)=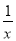 >0,此时g(x)在(0,+∞)上单调递增;
>0,此时g(x)在(0,+∞)上单调递增;
当a≠0时,只需g′(x)≥0在(0,+∞)上恒成立,因为x∈(0,+∞),只要2ax2-ax+1≥0,则需要a>0,
对于函数y=2ax2-ax+1,过定点(0,1),对称轴x=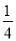 >0,只需Δ=a2-8a≤0,
>0,只需Δ=a2-8a≤0,
即0<a≤8.
综上a的取值范围是[0,8].


科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
已知命题p:“?x∈N*,x>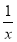 ”,命题p的否定为命题q,则q是“________”;q的真假为________(填“真”或“假”).
”,命题p的否定为命题q,则q是“________”;q的真假为________(填“真”或“假”).
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破五 高考解析几何(解析版) 题型:选择题
直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )
A.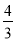 B.2 C.
B.2 C.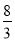 D.
D.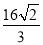
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破二 高考三角函数与平面向量(解析版) 题型:选择题
若复数z满足iz=2+4i,则在复平面内,z对应的点的坐标是( )
A.(2,4) B.(2,-4) C.(4,-2) D.(4,2)
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破三 高考数列(解析版) 题型:选择题
已知-9,a1,a2,a3,-1,成等差数列,-9,b1,b2,b3,-1成等比数列,则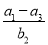 =( )
=( )
A.±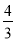 B.±
B.± C.-
C.-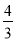 D.
D.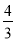
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破一 高考函数与导数(解析版) 题型:填空题
把一个周长为12 cm的长方形围成一个圆柱,当圆柱的体积最大时,该圆柱的底面周长与高的比是________.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省西安市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
最近,李师傅一家三口就如何将手中的10万块钱投资理财,提出了三种方案:
第一种方案:李师傅的儿子认为:根据股市收益大的特点,应该将10万块钱全部用来买股票. 据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利与亏损的概率均为 .
.
第二种方案:李师傅认为:现在股市风险大,基金风险较小,应将10万块钱全部用来买基金. 据分析预测:投资基金一年后可能获利20%,也可能损失10%,还可能不赔不赚,且这三种情况发生的概率分别为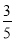 ,
,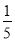 ,
,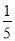 .
.
第三种方案:李师傅妻子认为:投入股市、基金均有风险,应该将10万块钱全部存入银行一年,现在存款年利率为4%,存款利息税率为5%.
针对以上三种投资方案,请你为李师傅家选择一种合理的理财方法,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省西安市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
若(x- )n的展开式中第3项的二项式系数是15,则
)n的展开式中第3项的二项式系数是15,则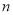 的值为( )
的值为( )
A.6 B.5 C.4 D.3
查看答案和解析>>
科目:高中数学 来源:2015届陕西省宝鸡市金台区高二下学期期末考试理科数学试卷(解析版) 题型:选择题
两个变量之间的线性相关程度越低,则其线性相关系数的数值( )
A.越小 B.越接近于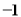 C.越接近于
C.越接近于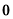 D.越接近于
D.越接近于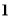
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com