练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．若3名女生，5名男生排成一排拍照，问：（用数字作答）
    （1）3名女生相邻的不同排法共有多少种？
    （2）3名女生不相邻的不同排法共有多少种？
    （3）5名男生顺序一定的不同排法有多少种？

    分析 （1）先把3名女生捆绑在一起看作一个复合函数，再和5名男生全排，可得结论；
    （2）先任意排5名男生形成了6个空，将3名女生插入到其中三个空中；
    （3）5名男生的顺序一定，在8个位置任意排3名女生

    解答 解：（1）先把3名女生捆绑在一起看作一个复合函数，再和5名男生全排，故有$A_3^3A_6^6=4320$，
    （2）先任意排5名男生形成了6个空，将3名女生插入到其中三个空中，故有$A_5^5A_6^3=14400$，
     （3）5名男生的顺序一定，在8个位置任意排3名女生，故有$A_8^3=336$

    点评 本题集排列多种类型于一题，充分体现了元素分析法（优先考虑特殊元素）、位置分析法（优先考虑特殊位置）、直接法、间接法（排除法）、捆绑法、等机会法、插空法等常见的解题思路．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．彩票公司每天开奖一次，从1，2，3，4四个号码中随机开出一个作为中奖号码，开奖时如果开出的号码与前一天相同，就要重开，直到开出与前一天不同的号码为止．如果第一天开出的号码是4，则第五天开出的号码也同样是4的概率为$\frac{7}{27}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若-$\frac{π}{2}$＜β＜0＜α＜$\frac{π}{2}$，cos（$\frac{π}{4}$+α）=$\frac{1}{3}$，cos（$\frac{π}{4}$-$\frac{β}{2}$）=$\frac{\sqrt{3}}{3}$，则cos（α+$\frac{β}{2}$）=$\frac{5\sqrt{3}}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

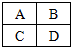    4．对如图中的A、B、C、D四个区域染色，每块区域染一种颜色，有公共边的区域不同色，现有红、黄、蓝三种不同颜色可以选择，则不同的染色方法共有（　　）
    A．12种B．18种C．20种D．22种

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．（x-2y）（x+y）8的展开式中，x2y7的系数为-48．（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知α∈（0，π），sin（α+$\frac{π}{6}$）=$\frac{1}{3}$，则cosα=（　　）
    A．$\frac{1+2\sqrt{6}}{6}$B．$\frac{1-2\sqrt{6}}{6}$C．$\frac{1±2\sqrt{6}}{6}$D．$\frac{-1-2\sqrt{6}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．从a，b，c这3个字母中取出2个按顺序排成一列，共有不同的排法（　　）
    A．4种B．6种C．12种D．3种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．化简：$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=（　　）
    A．sin2αB．cos2αC．tan2αD．cot2α

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．求下列圆的方程．
    （1）圆心是（4，-1），且过点（5，2）；
    （2）圆心在y轴上，半径为5，且过点（3，-4）；
    （3）过点P（2，-1）和直线x-y=1相切，并且圆心在直线y=-2x上．

    查看答案和解析>>

    同步练习册答案