
分析 (1)设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+b联立$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}+2{y}^{2}=1}\end{array}\right.$,整理得(2k2+1)x2+4kbx+2(b2-1)=0,由kFA+kFB=0,可得 b与k的关系,即可;
(2)由(1)得$\overrightarrow{FA}•\overrightarrow{FB}=({x}_{1}+1,{y}_{1})•({x}_{2}+1,{y}_{2})$=(x1+1)(x2+1)+(kx1+b)(kx2+b)
由=0及△求出b的范围.又d=$\sqrt{\frac{{b}^{2}}{{k}^{2}+1}}$=$\sqrt{\frac{{b}^{2}}{(\frac{3{b}^{2}-1}{4b})^{2}+1}}$=$\sqrt{\frac{16}{9+10(\frac{1}{b})^{2}+(\frac{1}{b})^{4}}}$$<\frac{4}{3}$即可求解,
解答 解:(1)设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+b
联立$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}+2{y}^{2}=1}\end{array}\right.$,整理得(2k2+1)x2+4kbx+2(b2-1)=0
${x}_{1}+{x}_{2}=\frac{-4kb}{2{k}^{2}+1},{x}_{1}{x}_{2}=\frac{2({b}^{2}-1)}{2{k}^{2}+1}$,△=8(2k2+1-b2)>0…①,
kFA+kFB=$\frac{{y}_{1}}{{x}_{1}+1}+\frac{{y}_{2}}{{x}_{2}+1}=\frac{(k{x}_{1}+b)({x}_{2}+1)+(k{x}_{2}+b)({x}_{1}+1)}{({x}_{1}+1)({x}_{2}+1)}$.
∴(kx2+b)(x1+1)+(kx1+b)(x2+1)=2kx1x2+(k+b)(x1+x2)+2b=2k×$\frac{2({b}^{2}-1)}{2{k}^{2}+1}$-(k+b)×$\frac{4kb}{2{k}^{2}+1}+2b$=0
∴b=2k,直线AB的方程为:y=kx+2k,
则动直线l一定经过一定点(-2,0).
(2)由(1)得$\overrightarrow{FA}•\overrightarrow{FB}=({x}_{1}+1,{y}_{1})•({x}_{2}+1,{y}_{2})$=(x1+1)(x2+1)+(kx1+b)(kx2+b)
=$(1+{k}^{2}){x}_{1}{x}_{2}+(kb+1)({x}_{1}+{x}_{2})+{b}^{2}+1$
=(k2+1)×$\frac{2({b}^{2}-1)}{2{k}^{2}+1}-(kb+1)×\frac{4kb}{2{k}^{2}+1}+{b}^{2}+1=0$.
∴$3{b}^{2}-4kb-1=0,k=\frac{3{b}^{2}-1}{4b}$代入①得①恒成立.
又d=$\sqrt{\frac{{b}^{2}}{{k}^{2}+1}}$=$\sqrt{\frac{{b}^{2}}{(\frac{3{b}^{2}-1}{4b})^{2}+1}}$=$\sqrt{\frac{16}{9+10(\frac{1}{b})^{2}+(\frac{1}{b})^{4}}}$$<\frac{4}{3}$,
∴d的取值范围(0,$\frac{4}{3}$).
点评 本题考查了直线与椭圆的位置关系,定点问题,及取值范围问题,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m>0,则x2+x-m=0没有实根 | B. | 若m<0,则x2+x-m=0没有实根 | ||
| C. | 若m≤0,则x2+x-m=0有实根 | D. | 若m≤0,则x2+x-m=0没有实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
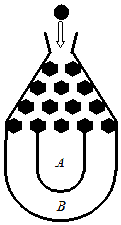 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
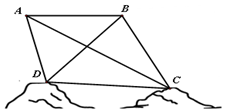 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.
为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com