
| A. | (16,21) | B. | (16,24) | C. | (17,21) | D. | (18,24) |
分析 根据图象可判断:$\frac{1}{2}$<a<1,1<b<2,2<c<4,6<d<8,当直线y=t,0<t<4,可以有4个交点,通过图象运动可以判断1×1×4×6=24,$\frac{1}{2}×2×2×8$=16,直线越往上走abcd的积越小,越往下abcd的积越大,即可求出答案.
解答 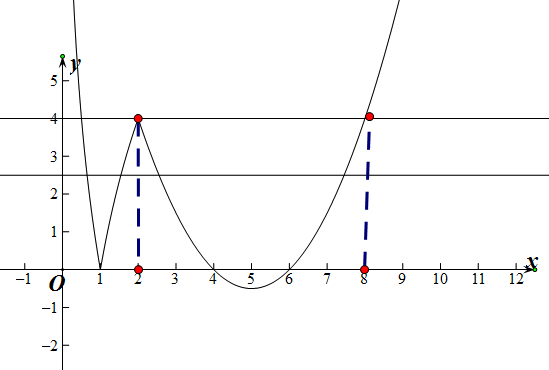 解:若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0
解:若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0
根据图象可判断:$\frac{1}{2}$<a<1,1<b<2,2<c<4,6<d<8,
当直线y=t,0<t<4,可以有4个交点,把直线向上平移,向下平移,可判断:直线越往上走abcd的积越小,越往下abcd的积越大,
当t=0时1×1×4×6=24,当t=4时,$\frac{1}{2}×2×2×8$=16,abcd的取值范围是(16,24),
故选:B.
点评 本题综合考查了函数图象的运用,求解两个图象的交点问题,运用动的观点解决,理解好题意是解题关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 19种 | C. | 32种 | D. | 60种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com