
(本小题满分14分)在棱长为2的正方体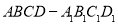 中,设
中,设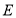 是棱
是棱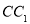 的中点。
的中点。

(1)求证: ;
;
(2)求证: 平面
平面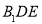 ;
;
(3)求三棱锥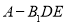 的体积.
的体积.
(1)(2)见解析;(3)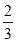
【解析】
试题分析:(1)(2)利用判定定理证明线面平行时,关键是在平面内找一条与已知直线平行的直线,解题时可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过平行线分线段成比例等;要证线线垂直,可通过征到线面垂直得到.(3)等体积法

试题解析:(1)连接BD,AE. 因四边形ABCD为正方形,故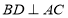 ,
,
因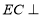 底面ABCD,
底面ABCD, 面ABCD,故
面ABCD,故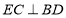 ,又
,又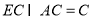 ,
,
故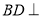 平面
平面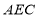 ,
,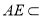 平面
平面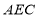 ,故
,故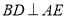 .
.
(2)连接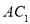 ,设
,设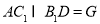 ,连接
,连接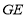 ,
,
则 为
为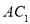 中点,而
中点,而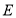 为
为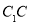 的中点,故
的中点,故 为三角形
为三角形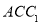 的中位线,
的中位线,
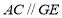 ,
,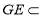 平面
平面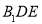 ,
, 平面
平面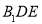 ,故
,故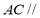 平面
平面 .
.
(3)由(2)知,点A到平面 的距离等于C到平面
的距离等于C到平面 的距离,
的距离,
故三棱锥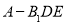 的体积
的体积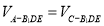 ,
,
而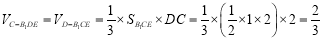 ,
,
三棱锥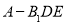 的体积为
的体积为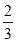 .
.
考点:线面、线线位置关系及几何体体积


 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2014-2015学年江西省赣州市十二县高二上学期期中联考文科数学试卷(解析版) 题型:选择题
设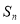 是等差数列
是等差数列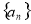 的前n项和,若
的前n项和,若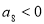 ,
,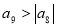 ,则使
,则使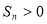 成立的最小正整数n为( )
成立的最小正整数n为( )
A.15 B.16 C.17 D.18
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北长阳县第一高中高二上学期期中考试文科数学试卷(解析版) 题型:填空题
如图,两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为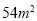 的直角梯形菜园(墙足够长),已知修筑篱笆每米的费用为50元,则修筑这个菜园的最少费用为 元.
的直角梯形菜园(墙足够长),已知修筑篱笆每米的费用为50元,则修筑这个菜园的最少费用为 元.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北长阳县第一高中高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知函数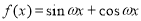 ,如果存在实数
,如果存在实数 ,使得对任意的实数
,使得对任意的实数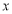 ,都有
,都有
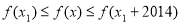 成立,则
成立,则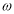 的最小正值为( )
的最小正值为( )
A.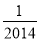 B.
B.  C.
C. D.
D.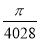
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北长阳县第一高中高二上学期期中考试理科数学试卷(解析版) 题型:填空题
一个几何体的三视图如图所示,则该几何体的体积为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com