
| 看电视 | 运动 | 合计 | |
| 男性 | 21 | ||
| 女性 | 43 | 70 | |
| 合计 | 124 |
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{4\sqrt{10}}}{5}$ | D. | $\frac{{8\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患感冒 | 不患感冒 | 合计 | |
| 活动时间超过1小时 | 20 | 40 | 60 |
| 活动时间低于1小时 | 30 | 10 | 40 |
| 合计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
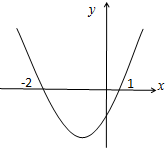 若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(-2),无极小值 | B. | 函数f(x)有极大值f(1),无极小值 | ||
| C. | 函数f(x)有极大值f(-2)和极小值f(1) | D. | 函数f(x)有极大值f(1)和极小值f(-2). |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2}$,0)U(0,$\sqrt{2}$) | B. | (-3$\sqrt{2}$,3$\sqrt{2}$) | C. | (-3$\sqrt{2}$,-$\sqrt{2}$)U($\sqrt{2}$,3$\sqrt{2}$) | D. | (-3$\sqrt{2}$,-$\sqrt{2}$]U($\sqrt{2}$,3$\sqrt{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com