
分析 (Ⅰ)由题意,得${a_n}=\frac{1}{2}n-\frac{2}{3}$,解$\frac{1}{2}n-\frac{2}{3}≥3$,得n的范围即可得出.
(Ⅱ)由题意,得an=2n-1,对于正整数,由an≥m,得$n≥\frac{m+1}{2}$.根据bm的定义可知当m=2k-1时,${b_m}=k({k∈{N^*}})$;当m=2k时,${b_m}=k+1({k∈{N^*}})$.∴b1+b2+…+b2m=(b1+b3+…+b2m-1)+(b2+b4+…+b2m),分组利用等差数列的求和公式即可得出.
(Ⅲ)假设存在p和q满足条件,由不等式pn+q≥m及p>0得$n≥\frac{m-q}{p}$.由于${b_m}=4m+1(m∈{N^*})$,根据bm的定义可知,对于任意的正整数m 都有$4m<\frac{m-q}{p}≤4m+1$,即-p-q≤(4p-1)m<-q对任意的正整数m都成立.对4p-1分类讨论即可得出.
解答 解:(Ⅰ)由题意,得${a_n}=\frac{1}{2}n-\frac{2}{3}$,解$\frac{1}{2}n-\frac{2}{3}≥3$,得$n≥\frac{22}{3}$.
∴$\frac{1}{2}n-\frac{2}{3}≥3$成立的所有n中的最小整数为8,即b3=8.
(Ⅱ)由题意,得an=2n-1,对于正整数,由an≥m,得$n≥\frac{m+1}{2}$.根据bm的定义可知当m=2k-1时,${b_m}=k({k∈{N^*}})$;当m=2k时,${b_m}=k+1({k∈{N^*}})$.
∴b1+b2+…+b2m=(b1+b3+…+b2m-1)+(b2+b4+…+b2m)=(1+2+3+…+m)+[2+3+4+…+(m+1)]=$\frac{{m({m+1})}}{2}+\frac{{m({m+3})}}{2}={m^2}+2m$.
(Ⅲ)假设存在p和q满足条件,由不等式pn+q≥m及p>0得$n≥\frac{m-q}{p}$.
∵${b_m}=4m+1(m∈{N^*})$,根据bm的定义可知,对于任意的正整数m 都有$4m<\frac{m-q}{p}≤4m+1$,即-p-q≤(4p-1)m<-q对任意的正整数m都成立.
当4p-1>0(或4p-1<0)时,得$m<-\frac{q}{4p-1}$(或$m≤-\frac{p+q}{4p-1}$),这与上述结论矛盾!当4p-1=0,即$p=\frac{1}{4}$时,得$-\frac{1}{4}-q≤0<-q$,解得$-\frac{1}{4}≤q<0$.
∴存在p和q,使得${b_m}=4m+1(m∈{N^*})$;p和q的取值范围分别是$p=\frac{1}{4}$,$-\frac{1}{4}≤q<0$.
点评 本题考查了等差数列与等比数列的定义通项公式与求和公式、不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于难题.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 看电视 | 运动 | 合计 | |
| 男性 | 21 | ||
| 女性 | 43 | 70 | |
| 合计 | 124 |
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-∞,-1)∪(2,+∞) | C. | [-1,2] | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
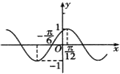
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=cos(4x-$\frac{π}{3}$) | D. | y=cos(2x-$\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com