
分析 (1)直线的方程为:y=kx+2,由题意可得:$\frac{|6k+2|}{\sqrt{1+{k}^{2}}}$≤2,解得k即可得出.
(2)假设存在常数k,使以AB为直径的圆过⊙C的圆心C,则$\overrightarrow{CA}•\overrightarrow{CB}$=0,直线方程与圆的方程联立,利用一元二次方程的根与系数的关系.
解答 解:(1)直线的方程为:y=kx+2,由题意可得:$\frac{|6k+2|}{\sqrt{1+{k}^{2}}}$≤2,解得$-\frac{3}{4}≤k≤0$.
(2)设A(x1,y1),B(x2,y2).
假设存在常数k,使以AB为直径的圆过⊙C的圆心C,则$\overrightarrow{CA}•\overrightarrow{CB}$=(x1-6)(x2-6)+y1y2=(x1-6)(x2-6)+(kx1+2)(kx2+2)
=(k2+1)x1x2+(2k-6)(x1+x2)+40=0.
联立$\left\{\begin{array}{l}{y=kx+2}\\{(x-6)^{2}+{y}^{2}=4}\end{array}\right.$,化为:(1+k2)x2+(4k-12)x+36=0.
∴x1+x2=$\frac{12-4k}{1+{k}^{2}}$,x1x2=$\frac{36}{1+{k}^{2}}$,
∴(k2+1)×$\frac{36}{1+{k}^{2}}$+(2k-6)$\frac{12-4k}{1+{k}^{2}}$+40=0.
化为8k2+12k+1=0.
解得k=$\frac{-3±\sqrt{7}}{4}$.
∵$-\frac{3}{4}≤k≤0$,∴k=$\frac{\sqrt{7}-3}{4}$.
存在常数k=$\frac{\sqrt{7}-3}{4}$,使以AB为直径的圆过⊙C的圆心C.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式、一元二次方程的根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
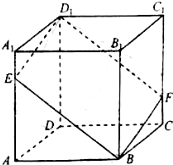 已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④
已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{2-2\sqrt{2},2}]$ | B. | (-∞,2] | C. | $[{2-2\sqrt{2},2})$ | D. | $({2-2\sqrt{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{4\sqrt{10}}}{5}$ | D. | $\frac{{8\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患感冒 | 不患感冒 | 合计 | |
| 活动时间超过1小时 | 20 | 40 | 60 |
| 活动时间低于1小时 | 30 | 10 | 40 |
| 合计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com