
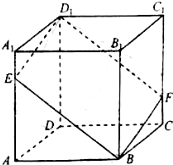
 已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④
已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④分析 设正方体的棱长为a,由图形可知,当x=0或x=a时,四边形BFD1E的面积取得最大值为$\sqrt{2}{a}^{2}$,当x=$\frac{a}{2}$时,四边形BFD1E的面积有最小值为$\frac{\sqrt{6}}{2}{a}^{2}$,由此判断①错误,③正确;再利用等积法证明四棱锥B1-BFD1E的体积与x取值无关,说明②错误,④正确.
解答 解:由图可知,四边形BFD1E是平行四边形,
设正方体的棱长为a,AE=x(0≤x≤a),
则当x=0或x=a时,四边形BFD1E的面积取得最大值为$\sqrt{2}{a}^{2}$,
当x=$\frac{a}{2}$时,四边形BFD1E的面积有最小值为$\frac{\sqrt{6}}{2}{a}^{2}$.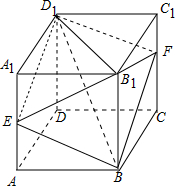
∴①错误,③正确;
四棱锥B1-BED1F的体积等于${V}_{{D}_{1}-B{B}_{1}E}+{V}_{{D}_{1}-B{B}_{1}F}$,
∵三角形BB1E的面积为$\frac{1}{2}{a}^{2}$为定值,三棱锥D1-BB1E的高D1C1=a,
三角形BB1F的面积为$\frac{1}{2}{a}^{2}$为定值,三棱锥D1-BB1F的高为D1A1=a,
∴三棱锥D1-BB1E和三棱锥D1-BB1F体积为定值,
即四棱锥B1-BED1F的体积为定值,
∴②错误,④正确.
∴正确命题的序号是③④.
故答案为:③④.
点评 本题考查命题的真假判断与应用,考查了利用等积法求多面体的体积,考查空间想象能力和思维能力,是中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
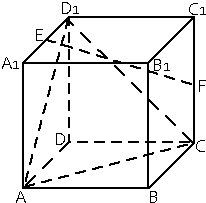 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-∞,-1)∪(2,+∞) | C. | [-1,2] | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com