
分析 (Ⅰ)由an+1=2an+1变形为:an+1+1=2(an+1).利用等比数列的通项公式即可得出.
(Ⅱ)$\frac{1}{2}$-$\frac{{a}_{n}}{{a}_{n+1}}$=$\frac{1}{2}$-$\frac{{2}^{n}-1}{{2}^{n+1}-1}$=$\frac{1}{2({2}^{n+1}-1)}$,即证:$\frac{1}{6}≤\sum{(\frac{1}{2}-\frac{{{2^n}-1}}{{{2^{n+1}}-1}})}<\frac{1}{3}$.利用数列的单调性及其放缩法即可证明.
解答 (Ⅰ)解:由an+1=2an+1变形为:an+1+1=2(an+1).
∴数列{an+1}是等比数列,公比为2,首项为2.
∴an+1=2n.
∴${a_n}={2^n}-1$.
(Ⅱ)证明:$\frac{1}{2}$-$\frac{{a}_{n}}{{a}_{n+1}}$=$\frac{1}{2}$-$\frac{{2}^{n}-1}{{2}^{n+1}-1}$=$\frac{1}{2({2}^{n+1}-1)}$,即证:$\frac{1}{6}≤\sum{(\frac{1}{2}-\frac{{{2^n}-1}}{{{2^{n+1}}-1}})}<\frac{1}{3}$.
一方面,∵$\frac{1}{{2({2^{n+1}}-1)}}>0$,∴$\sum{(\frac{1}{2}-\frac{{{2^n}-1}}{{{2^{n+1}}-1}})}$递增,∴$\sum{(\frac{1}{2}-\frac{{{2^n}-1}}{{{2^{n+1}}-1}})}≥\frac{1}{2}-\frac{{{2^1}-1}}{{{2^{1+1}}-1}}=\frac{1}{6}$.
另一方面,先证:$\frac{1}{{2({2^{n+1}}-1)}}≤\frac{1}{6}•\frac{1}{{{2^{n-1}}}}$,
∴$\sum{(\frac{1}{2}-\frac{{{2^n}-1}}{{{2^{n+1}}-1}})}≤\frac{1}{3}(1-\frac{1}{2^n})<\frac{1}{3}$,
综上可得:$\frac{n}{2}$-$\frac{1}{3}$<$\frac{{a}_{1}}{{a}_{2}}$+$\frac{{a}_{2}}{{a}_{3}}$+…+$\frac{{a}_{n}}{{a}_{n+1}}$≤$\frac{n}{2}$-$\frac{1}{6}$.
点评 本题考查了等比数列的通项公式与求和公式、放缩法、数列的单调性,考查了等价转化方法、推理能力与计算能力,属于难题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
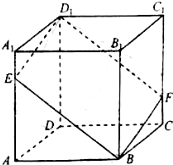 已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④
已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{2-2\sqrt{2},2}]$ | B. | (-∞,2] | C. | $[{2-2\sqrt{2},2})$ | D. | $({2-2\sqrt{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{4\sqrt{10}}}{5}$ | D. | $\frac{{8\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
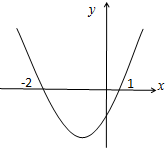 若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(-2),无极小值 | B. | 函数f(x)有极大值f(1),无极小值 | ||
| C. | 函数f(x)有极大值f(-2)和极小值f(1) | D. | 函数f(x)有极大值f(1)和极小值f(-2). |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com