
分析 由题意,BC的中点O′是△DBC外接圆的圆心,设球心为O,OO′=d,球的半径为R,则由勾股定理可得R2=d2+($\sqrt{3}$)2=12+($\sqrt{2}$-d)2,求出球的半径,即可求出球O的体积.
解答 解:由题意,BC的中点O′是△DBC外接圆的圆心,设球心为O,OO′=d,球的半径为R,则
由勾股定理可得R2=d2+($\sqrt{3}$)2=12+($\sqrt{2}$-d)2,∴R=$\sqrt{3}$,
∴球O的体积为$\frac{4}{3}•(\sqrt{3})^{3}$=4$\sqrt{3}$π.
故答案为4$\sqrt{3}$π.
点评 本题考查球O的体积,考查学生的计算能力,求出球O的半径是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-∞,-1)∪(2,+∞) | C. | [-1,2] | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
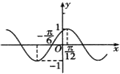
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=cos(4x-$\frac{π}{3}$) | D. | y=cos(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
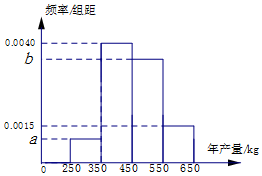 某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.
某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p?Q | B. | P∩Q=∅ | C. | P∪Q=Q | D. | CRP=Q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com