
���� ��1����ȥ�����ɵ�ԲC����ͨ���̣�
��2�����ü�������ֱ������Ļ�����������ֱ��l�ļ����귽�̻�Ϊֱ�����귽�̣�
��3�����P��Բ�����߳�Ϊd����d2=|PA|•|PB|����|PA|•|PB|����Сֵ������Բ�����߳�����Сֵ��
��� �⣺��1��ԲC�IJ�������Ϊ$\left\{\begin{array}{l}x=3+2cos��\\ y=2sin��\end{array}\right.$����Ϊ����������ͨ����Ϊ��x-3��2+y2=4��
��2��ֱ��l�ļ����귽��Ϊ��cos��+��sin��+1=0��ֱ�����귽��x+y+1=0��
��3�����P��Բ�����߳�Ϊd����d2=|PA|•|PB|��
��|PA|•|PB|����Сֵ������Բ�����߳�����Сֵ��
Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$����Բ�����߳�����Сֵ=$\sqrt{8+4}$=2$\sqrt{3}$��
��|PA|•|PB|����СֵΪ12��
���� ���⿼����ֱ�����귽�̻�Ϊ�������̡������귽�̻�Ϊֱ�����귽�̡��㵽ֱ�ߵľ��빫ʽ��ֱ����Բ��λ�ù�ϵ��������������������������������е��⣮


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{{4\sqrt{5}}}{5}$ | C�� | $\frac{{4\sqrt{10}}}{5}$ | D�� | $\frac{{8\sqrt{10}}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
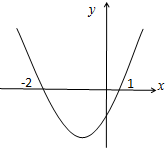 ������f��x����R�Ͽɵ����䵼����Ϊf�䣨x�����Һ���y=��1-x��f�䣨x����ͼ����ͼ��ʾ�������н�����һ���������ǣ�������
������f��x����R�Ͽɵ����䵼����Ϊf�䣨x�����Һ���y=��1-x��f�䣨x����ͼ����ͼ��ʾ�������н�����һ���������ǣ�������| A�� | ����f��x���м���ֵf��-2������Сֵ | B�� | ����f��x���м���ֵf��1������Сֵ | ||
| C�� | ����f��x���м���ֵf��-2���ͼ�Сֵf��1�� | D�� | ����f��x���м���ֵf��1���ͼ�Сֵf��-2���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-$\sqrt{2}$��0��U��0��$\sqrt{2}$�� | B�� | ��-3$\sqrt{2}$��3$\sqrt{2}$�� | C�� | ��-3$\sqrt{2}$��-$\sqrt{2}$��U��$\sqrt{2}$��3$\sqrt{2}$�� | D�� | ��-3$\sqrt{2}$��-$\sqrt{2}$]U��$\sqrt{2}$��3$\sqrt{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com