
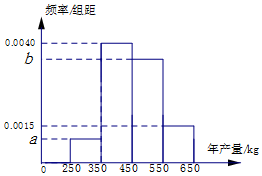
 某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.
某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.分析 (1)由频率分布直方图的性质列出方程组,能求出图中a,b的值.
(2)当年产量大于250kg而低于300kg,或年产量大于350kg而低于400kg,或年产量大于550kg而低于600kg时,其年销售额为大于5000而低于6000元,由此能估计年销售额大于5000元小于6000元的概率.
解答 解:(1)由已知,得:
$\left\{\begin{array}{l}{100(a+0.015+b+0.0040)=1}\\{300×100a+400×0.4+500×100b+600×0.15=455}\end{array}\right.$,
即$\left\{\begin{array}{l}{100(a+b)=0.45}\\{300a+500b=2.05}\end{array}\right.$,
解得a=0.001,b=0.0035.(6分)
(2)由(1)结合直方图可知,
当年产量大于250kg而低于300kg,
或年产量大于350kg而低于400kg,
或年产量大于550kg而低于600kg时,
其年销售额为大于5000而低于6000元,
所以估计年销售额大于5000元小于6000元的概率为50×(0.001+0.004+0.0015)=0.325.(12分)
点评 本小题主要考查学生对概率知识的理解,以及统计案例的相关知识,同时考查学生的数据处理能力.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
| 患感冒 | 不患感冒 | 合计 | |
| 活动时间超过1小时 | 20 | 40 | 60 |
| 活动时间低于1小时 | 30 | 10 | 40 |
| 合计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-8,b=-10 | B. | a=-4,b=-9 | C. | a=-1,b=9 | D. | a=-1,b=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2}$,0)U(0,$\sqrt{2}$) | B. | (-3$\sqrt{2}$,3$\sqrt{2}$) | C. | (-3$\sqrt{2}$,-$\sqrt{2}$)U($\sqrt{2}$,3$\sqrt{2}$) | D. | (-3$\sqrt{2}$,-$\sqrt{2}$]U($\sqrt{2}$,3$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 定义实数a,b间的计算法则如下a△b=$\left\{\begin{array}{l}a,\;\;a≥b\\{b^2},a<b\end{array}$.
定义实数a,b间的计算法则如下a△b=$\left\{\begin{array}{l}a,\;\;a≥b\\{b^2},a<b\end{array}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com