
 定义实数a,b间的计算法则如下a△b=$\left\{\begin{array}{l}a,\;\;a≥b\\{b^2},a<b\end{array}$.
定义实数a,b间的计算法则如下a△b=$\left\{\begin{array}{l}a,\;\;a≥b\\{b^2},a<b\end{array}$.分析 (1)先求出3△1,再求出2△(3△1)的值即可;
(2)分别求出x△(y△z)和(x△y)△z的值,讨论y2与z的大小即可;
(3)讨论x的大小,分x≥2,x<1,1≤x<2,求得函数式,画出函数图象,即可得到该函数单调递增区间和值域.
解答 解:(1)实数a,b间的计算法则如下a△b=$\left\{\begin{array}{l}a,\;\;a≥b\\{b^2},a<b\end{array}$.
则2△(3△1)=2△3=32=9;
(2)对0<x<z<y的任意实数x,y,z,
x△(y△z)=x△y=y2,
(x△y)△z=y2△z,
此时若y2≥z,则(x△y)△z=y2;
若y2<z,则(x△y)△z=z2.
即若y2≥z,则x△(y△z)=(x△y)△z;
若y2<z,则x△(y△z)>(x△y)△z.
(3)当x>2时,y=(1△x)+(2△x)=x2+x2=2x2;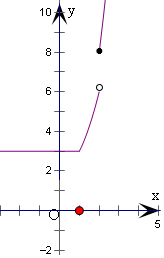
当1<x≤2时,y=(1△x)+(2△x)=x2+2;
当x≤1时,y=(1△x)+(2△x)=1+2=3.
即有y=$\left\{\begin{array}{l}{3,x≤1}\\{{x}^{2}+2,1<x≤2}\\{2{x}^{2},x≥2}\end{array}\right.$,
画出函数y的图象,如右:
该函数单调递增区间为(1,2),(2,+∞);
值域为[3,+∞).
点评 本题考查了新定义的理解和运用,考查分类讨论思想方法,以及数形结合思想方法,是一道中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
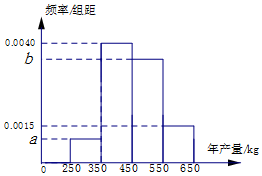 某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.
某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p?Q | B. | P∩Q=∅ | C. | P∪Q=Q | D. | CRP=Q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值3,无最大值 | B. | 有最小值5,无最大值 | ||
| C. | 有最大值3,无最小值 | D. | 有最大值5,无最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
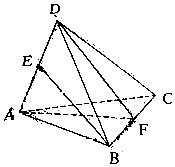 如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8$\sqrt{6}$π | B. | $\sqrt{6}$π | C. | 24π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | a<b<c | C. | b<a<c | D. | a<c<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com