
| A. | a=-8,b=-10 | B. | a=-4,b=-9 | C. | a=-1,b=9 | D. | a=-1,b=2 |
分析 分别求解不等式$\frac{4x+1}{x+2}$<0和不等式ax2+bx-2>0的解集,它们解集相同,可求a、b的值.
解答 解:不等式$\frac{4x+1}{x+2}$<0等价于(4x+1)(x+2)<0,
解得:$-2<x<-\frac{1}{4}$,
∵解集相同,
∴不等式ax2+bx-2>0的解集为$-2<x<-\frac{1}{4}$,
由方程与不等式的关系可知:ax2+bx-2=0的根为:${x}_{1}=-2,{x}_{2}=-\frac{1}{4}$,
由韦达定理:$\left\{\begin{array}{l}{{x}_{1}{x}_{2}=-\frac{2}{a}}\\{{x}_{1}+{x}_{2}=-\frac{b}{a}}\end{array}\right.$,解得:a=-4,b=-9,
故选:B.
点评 本题考察了分式不等式的解法和方程与不等式的关系,属于基础题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
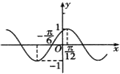
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=cos(4x-$\frac{π}{3}$) | D. | y=cos(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
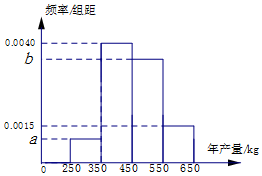 某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.
某人种植一种经济作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg,已知当年产量低于350kg时,单位售价为20元/kg,若当年产量不低于350kg而低于550时,单位售价为15元/kg,当年产量不低于550kg时,单位售价为10元/kg.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=80,b=61,A=60° | B. | a=10,b=14,A=30° | ||
| C. | b=23,A=45°,B=30° | D. | a=61,c=47,A=120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com