Question

19．已知函数f（x）=$\frac{1}{3}$x³+$\frac{1}{2}$ax²+bx在区间[-1，1）、（1，3]内各有一个极值点，则a-4b的取值范围是（-16，10]．

Answer 1

分析 求导函数，利用f（x）的两个极值点分别是x₁，x₂，x₁∈[-1，1），x₂∈（1，3]，建立不等式，利用平面区域，即可求a-4b的取值范围．

解答 解：由题意，f′（x）=x²+ax+b，
∵f（x）的两个极值点分别是x₁，x₂，
x₁∈（-1，1），x₂∈（1，3），
∴$\left\{\begin{array}{l}{f′（-1）=1-a+b＞0}\\{f′（1）=1+a+b＜0}\\{f′（3）=9+3a+b＞0}\end{array}\right.$，
对应的平面区域如图所示：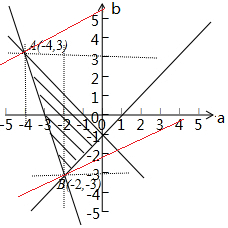

令z=a-4b，得：b=$\frac{1}{4}$a-$\frac{1}{4}$z，
平移直线b=b=$\frac{1}{4}$a-$\frac{1}{4}$z，
显然直线过A（-4，3）时，z最小，最小值是-16，
过B（-2，-3）时，z最大，最大值是10，
故答案为：（-16，10]．

点评 本题考查导数知识的运用，考查平面区域的运用，考查学生的计算能力，属于中档题．