
分析 (I)设等比数列{an}的公比为q,由b3=6+b2.可得b3-b2=6.由数列{an}和{bn}满足a1a2…an=($\sqrt{2}$)${\;}^{{b}_{n}}$,n∈N*,n≥2时,利用递推关系可得:an=$(\sqrt{2})^{{b}_{n}-{b}_{n-1}}$,可得a3=$(\sqrt{2})^{{b}_{3}-{b}_{2}}$=8.利用等比数列的通项公式可得an.进而得到bn.
(Ⅱ)(i)cn=$\frac{1}{{a}_{n}}$-$\frac{1}{{b}_{n}}$=$\frac{1}{{2}^{n}}$-$\frac{1}{n(n+1)}$=$\frac{1}{{2}^{n}}$-$(\frac{1}{n}-\frac{1}{n+1})$,利用等比数列的前n项和公式及其“裂项求和”方法可得数列{cn}的前n项和为Sn.
(ii)n≤4时,cn>0.当n≥5时,cn=$\frac{1}{n(n+1)}$$[\frac{n(n+1)}{{2}^{n}}-1]$<0,即可得出.
解答 解:(I)设等比数列{an}的公比为q,
∵b3=6+b2.∴b3-b2=6.
∵数列{an}和{bn}满足a1a2…an=($\sqrt{2}$)${\;}^{{b}_{n}}$,n∈N*,
∴n≥2时,a1a2…an-1=$(\sqrt{2})^{{b}_{n-1}}$,可得:an=$(\sqrt{2})^{{b}_{n}-{b}_{n-1}}$,
∴a3=$(\sqrt{2})^{{b}_{3}-{b}_{2}}$=$(\sqrt{2})^{6}$=8.
又a1=2,∴8=2q2,解得q=2(-2舍去).
∴an=2×2n-1=2n.
∴($\sqrt{2}$)${\;}^{{b}_{n}}$=21+2+…+n=${2}^{\frac{n(n+1)}{2}}$,
∴bn=n(n+1).
(Ⅱ)(i)cn=$\frac{1}{{a}_{n}}$-$\frac{1}{{b}_{n}}$=$\frac{1}{{2}^{n}}$-$\frac{1}{n(n+1)}$=$\frac{1}{{2}^{n}}$-$(\frac{1}{n}-\frac{1}{n+1})$,
∴数列{cn}的前n项和为Sn=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$(1-\frac{1}{n+1})$=$\frac{1}{n+1}$-$\frac{1}{{2}^{n}}$.
(ii)c1=0,c2=$\frac{1}{12}$,c3=$\frac{1}{24}$,c4=$\frac{1}{{2}^{4}}$-$\frac{1}{20}$=$\frac{1}{80}$.
当n≥5时,cn=$\frac{1}{n(n+1)}$$[\frac{n(n+1)}{{2}^{n}}-1]$.
由$\frac{(n+1)(n+2)}{{2}^{n+1}}$-$\frac{n(n+1)}{{2}^{n}}$=$\frac{(2-n)(n+1)}{{2}^{n+1}}$<0,
∴cn<0.
若Sk≥Sn恒成立,
∴k=4.
点评 本题考查了递推关系、等比数列与等差数列的通项公式及其前n项和公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
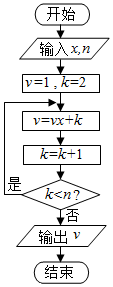 如图所示的程序框图的算法思路源于我国古代数字著作《数书九章》,称为“秦九韶算法”.执行该程序框图,若输入x=2,n=5,则输出的v=( )
如图所示的程序框图的算法思路源于我国古代数字著作《数书九章》,称为“秦九韶算法”.执行该程序框图,若输入x=2,n=5,则输出的v=( )| A. | 26 | B. | 48 | C. | 57 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
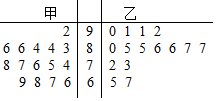 某农场用甲、乙两种不同的方式培育了一批甘蔗苗,培育一段时间后,同时随机抽取两种方式培育的甘蔗苗各15株,测量其高度,得到如图的茎叶图(单位:cm)
某农场用甲、乙两种不同的方式培育了一批甘蔗苗,培育一段时间后,同时随机抽取两种方式培育的甘蔗苗各15株,测量其高度,得到如图的茎叶图(单位:cm)| 甲方式 | 乙方式 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | ($\frac{1}{2}$,1] | C. | (0,$\frac{1}{2}$] | D. | (-∞,$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com