
【题目】二次函数f(x)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
【答案】
(1)解:设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
因为f(x+1)﹣f(x)=2x,所以a(x+1)2+b(x+1)+1﹣(ax2+bx+1)=2x.
即2ax+a+b=2x,所以 ![]() ,∴
,∴ ![]() ,
,
所以f(x)=x2﹣x+1
(2)解:由题意得x2﹣x+1>2x+m在[﹣1,1]上恒成立.即x2﹣3x+1﹣m>0在[﹣1,1]上恒成立.
设g(x)=x2﹣3x+1﹣m,其图象的对称轴为直线 ![]() ,所以g(x)在[﹣1,1]上递减.
,所以g(x)在[﹣1,1]上递减.
故只需最小值g(1)>0,即12﹣3×1+1﹣m>0,
解得m<﹣1
【解析】(1)先设f(x)=ax2+bx+c,在利用f(0)=1求c,再利用两方程相等对应项系数相等求a,b即可.(2)转化为x2﹣3x+1﹣m>0在[﹣1,1]上恒成立问题,找其在[﹣1,1]上的最小值让其大于0即可.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C与x轴相切,圆心C在射线3x﹣y=0(x>0)上,直线x﹣y=0被圆C截得的弦长为2 ![]()
(1)求圆C标准方程;
(2)若点Q在直线l1:x+y+1=0上,经过点Q直线l2与圆C相切于p点,求|QP|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2
B.6
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 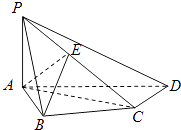
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,求: 
(1)直线PQ与CD所成角的大小
(2)四面体PCDQ的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= ![]() .
.
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦;
(Ⅲ)求点E到平面ACD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com