
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() .且
.且![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 重心.
重心.
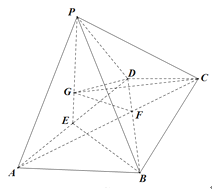
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)方法一:连接![]() 并延长与
并延长与![]() 交于
交于![]() ,连接
,连接![]() ,推导出
,推导出![]() ,从而
,从而![]() ,由
,由![]() 为
为![]() 重心,得
重心,得![]() ,进而
,进而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
方法二:过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,易知
,易知![]() ,又
,又![]() 为
为![]() 的重心, 根据比例关系可得
的重心, 根据比例关系可得 ![]() ,
,
又![]() 为梯形,
为梯形, ![]() ,由比例关系可得
,由比例关系可得![]() ,又
,又![]() ,
, ![]() 得
得![]() ,
, ![]() 为平行四边形,可得
为平行四边形,可得![]() ,根据线面平行判定定理即可证明结果;
,根据线面平行判定定理即可证明结果;
方法三:过![]() 作
作![]()
![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,由
,由![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点,且
的中点,且![]() ,
, ![]() 为
为![]() 的重心,
的重心,![]()
又由梯形![]() ,可得
,可得![]() ,可证
,可证 ![]() ,可得平面
,可得平面![]() 平面
平面![]()
根据面面平行的性质即可证明结果.
(2)方法一:由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点,可得
的中点,可得![]() 平面
平面![]() ,且
,且![]() ,由(1)知
,由(1)知![]()
![]() 平面
平面![]() ,可得
,可得![]() ,再根据题意解出
,再根据题意解出![]() ,即可求出结果.
,即可求出结果.
方法二:三棱锥![]() 的体积
的体积![]() .由此能求出结果.
.由此能求出结果.
(1)方法一:连![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
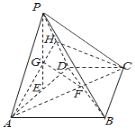
由梯形![]() ,
, ![]() 且
且![]() ,知
,知![]()
又![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() 为
为![]() 的重心,∴
的重心,∴![]()
在![]() 中,
中,![]() ,故
,故![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
方法二:过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
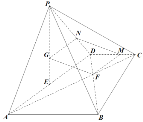
![]()
![]() 为
为![]() 的中点,且
的中点,且![]() ,
,
![]() 为
为![]() 的重心,
的重心, ![]() ,
, ![]() ,
,
又![]() 为梯形,
为梯形, ![]() ,
,![]() ,
, ![]()
![]() ,
, ![]() ,
,![]()
又由所作![]() ,
, ![]() 得
得![]() ,
, ![]() 为平行四边形.
为平行四边形.
![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]()
![]() 面
面![]()
方法三:过![]() 作
作![]()
![]()
![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
由![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点,且
的中点,且![]() ,
, ![]() 为
为![]() 的重心,
的重心,
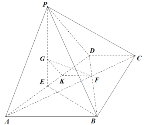
得![]() ,
,![]()
![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,
,
知![]() ,即
,即![]()
∴在![]() 中,
中, ![]() ,所以平面
,所以平面![]() 平面
平面![]()
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]()
(2)方法一:由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点
的中点
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由(1)知![]()
![]() 平面
平面![]() ,∴
,∴![]()
又由梯形![]() ,
, ![]() ,且
,且![]() ,知
,知![]()
又![]() 为正三角形,得
为正三角形,得![]() ,
,
∴![]()
得![]()
∴三棱锥![]() 的体积为
的体积为![]() .
.
方法二:由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点
的中点
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由![]() ,∴
,∴![]()
而又![]() 为正三角形,得
为正三角形,得![]() ,得
,得![]() .
.
∴![]()
![]() ,∴三棱锥
,∴三棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中,
中,![]() ,
,![]() ,由顶点
,由顶点![]() 沿棱柱侧面经过棱
沿棱柱侧面经过棱![]() 到顶点
到顶点![]() 的最短路线与棱
的最短路线与棱![]() 的交点记为
的交点记为![]() ,求:
,求:

(1)三棱柱的侧面展开科的对角线长;
(2)该最短路线的长及![]() 的值;
的值;
(3)平面![]() 与平面
与平面![]() 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一张半径为1米的圆形铁皮,工人师傅需要剪一块顶角为锐角的等腰三角形![]() ,不妨设
,不妨设 ![]() ,
, ![]() 边上的高为
边上的高为 ![]() ,圆心为
,圆心为 ![]() ,为了使三角形的面积最大,我们设计了两种方案.
,为了使三角形的面积最大,我们设计了两种方案.

(1)方案1:设 ![]() 为
为 ![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积 ![]() ; 方案2:设
; 方案2:设![]() 的高
的高![]() 为
为![]() ,用
,用![]() 表示
表示 ![]() 的面积
的面积![]() ;
;
(2)请从(1)中的两种方案中选择一种,求出![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海轮以每小时30海里的速度航行,在点![]() 测得海面上油井
测得海面上油井![]() 在南偏东
在南偏东![]() ,海轮向北航行40分钟后到达点
,海轮向北航行40分钟后到达点![]() ,测得油井
,测得油井![]() 在南偏东
在南偏东![]() ,海轮改为北偏东
,海轮改为北偏东![]() 的航向再行驶80分钟到达点
的航向再行驶80分钟到达点![]() ,则
,则![]() 两点的距离为(单位:海里)
两点的距离为(单位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com