
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据充要条件的定义,可判断①;根据函数奇偶性的定义,可判断②;根据函数图象的平移变换法则,可判断③;写出原命题的逆命题,可判断④;根据复合命题真假判断的真值表,可判断⑤;分析函数零点的位置,可判断⑥.
解答 解:①方程ax2+x+1=0有且只有一个实根的充要条件是a=$\frac{1}{4}$,或a=0,故错误;
②函数y=$\sqrt{{x}^{2}-1}$+$\sqrt{1-{x}^{2}}$=0,(x=±1)即是偶函数,也是奇函数,故错误;
③函数f(x)=(2x-3)2+1=[2(x+1)-5]2+1的图象是由函数y=(2x-5)2+1的图象向左平移1个单位得到的,故正确;
④命题“若x,y都是偶数,则x+y也是偶数”的逆命题为命题“若x+y是偶数,则x,y都是偶数”,是假命题,故错误;
⑤已知p,q是简单命题,若p∨q是真命题,则p,q可能一真一假,此时p∧q是假命题,故错误;
⑥若函数f(x)=|ax-1|-log2(x+2),(a>1)有两个零点x1,x2,
则-1<x1<0,x1+2>1,
x2>0,x2+2>2
则(x1+2)(x2+2)>2>1,故正确;
故选:A
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的奇偶性,充要条件,函数的零点,四种命题的否定等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{3}$ | C. | 5或6 | D. | 6或$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10] | B. | $(\frac{1}{2},1)∪(1,5]$ | C. | $(\frac{1}{2},5]$ | D. | (1,2)∪(2,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
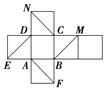 如图所示是正方体的平面展开图,在这个正方体中,其中正确的命题有( )
如图所示是正方体的平面展开图,在这个正方体中,其中正确的命题有( )| A. | ①②③ | B. | ②④ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-3x-1 | B. | x2+3x-1 | C. | -x2+3x+1 | D. | -x2-3x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com