
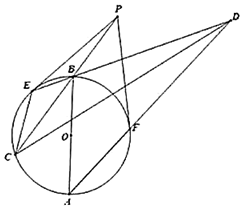
分析 连接AE,OE,OF,PD.可得∠AEB=∠OEP=∠OFP=90°,OE=OB=OA=OF,∠OEF=∠OFE=$\frac{1}{2}$∠EPF,∠PEB=∠PCE,∠OEB=∠OBE.可得:点D在以P为圆心,PE的长为半径的圆上.进而证明E,C,D,P四点共圆,即可得出结论.
解答 证明:连接AE,OE,OF,PD.可得∠AEB=∠OEP=∠OFP=90°,OE=OB=OA=OF,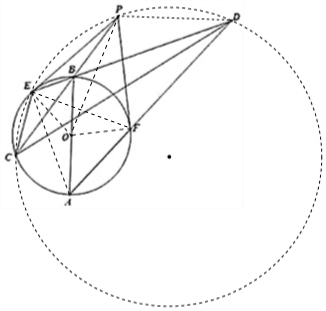
∠OEF=∠OFE=$\frac{1}{2}$∠EPF,∠PEB=∠PCE,
∠OEB=∠OBE.
∵∠EDA=∠EBA-∠BAD=∠BEO-∠BEF=∠OEF=$\frac{1}{2}∠EPF$,PE=PF.
∴点D在以P为圆心,PE的长为半径的圆上.
∴PE=PD,∴∠PED=∠PDE,∠ECP=∠PDE,
∴E,C,D,P四点共圆,
∴∠PED=∠PCD.
∴∠PCD=∠PCE.
点评 本题考查了圆的性质、圆的切线的性质、四点共圆,本题条件比较多,考查了较强的推理能力与计算能力,属于难题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,±3) | B. | (±3,0) | C. | (±1,0) | D. | (0,±1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ③ | C. | ①④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
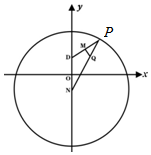 如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.
如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥b,b∥α,则a∥α | C. | 若a⊥α,b⊥α,则a∥b | D. | 若a⊥α,b⊥a,则b⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com