
【题目】已知点A是圆C:x2+y2+ax+4y+10=0上任意一点,点A关于直线x+2y-1=0的对称点也在圆C上,则实数a的值为( )
A.10
B.-10
C.-4
D.4
【答案】B
【解析】通过配方可得圆C的标准方程为(x+ ![]() )2+(y+2)2=
)2+(y+2)2= ![]() ,由题意,可知直线x+2y-1=0过圆心C(-
,由题意,可知直线x+2y-1=0过圆心C(- ![]() ,-2),∴-
,-2),∴- ![]() -4-1=0,∴a=-10.又a=-10时,
-4-1=0,∴a=-10.又a=-10时, ![]() >0,∴a的值为-10,
>0,∴a的值为-10,
所以答案是:B.
【考点精析】解答此题的关键在于理解圆的标准方程的相关知识,掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程,以及对圆的一般方程的理解,了解圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.
;圆心为A(a,b),半径为r的圆的方程,以及对圆的一般方程的理解,了解圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.


科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.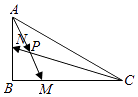
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,其离心率
,其离心率 ![]() ,点
,点 ![]() 为椭圆上的一个动点,△
为椭圆上的一个动点,△ ![]() 面积的最大值为
面积的最大值为 ![]() .
.
(1)求椭圆的标准方程;
(2)若 ![]() 是椭圆上不重合的四个点,
是椭圆上不重合的四个点, ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,
, ![]() 求
求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组有9名学生.若从9名学生中选取3人,则选取的3人中恰好有一个女生的概率是 ![]() .
.
(1)该小组中男女学生各多少人?
(2)9个学生站成一列队,现要求女生保持相对顺序不变(即女生 前后顺序保持不变)重新站队,问有多少种重新站队的方法?(要求用数字作答)
(3)9名学生站成一列,要求男生必须两两站在一起,有多少种站队的方法?(要求用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆O的周长和面积同时等分成两部分的函数称为圆煌一个“太极函数”下列有关说法中: 
①对圆O:x2+y2=1的所有非常数函数的太极函数中,一定不能为偶函数;
②函数f(x)=sinx+1是圆O:x2+(y﹣1)2=1的一个太极函数;
③存在圆O,使得f(x)= ![]() 是圆O的太极函数;
是圆O的太极函数;
④直线(m+1)x﹣(2m+1)y﹣1=0所对应的函数一定是圆O:(x﹣2)2+(y﹣1)2=R2(R>0)的太极函数.
所有正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为正方形的四棱锥S﹣ABCD,且SD⊥平面ABCD,SD= ![]() ,AB=1,线段SB上一M点满足
,AB=1,线段SB上一M点满足 ![]() =
= ![]() ,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() : x2+y2+Dx+Ey+3=0 ,圆
: x2+y2+Dx+Ey+3=0 ,圆 ![]() 关于直线 x+y-1=0对称,圆心在第二象限,半径为
关于直线 x+y-1=0对称,圆心在第二象限,半径为![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)已知不过原点的直线 l 与圆 ![]() 相切,且在
相切,且在 ![]() 轴、
轴、 ![]() 轴上的截距相等,求直线 l 的方程.
轴上的截距相等,求直线 l 的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com