
| A. | 3 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 由题意画出图形,利用$\overline{P{F}_{1}}$⊥$\overline{P{F}_{2}}$及△PF1F2的面积为9列式求得|PF1||PF2|=18.再由勾股定理及椭圆定义即可求得b.
解答 解:如图,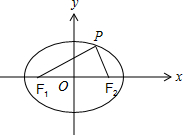
∵$\overline{P{F}_{1}}$⊥$\overline{P{F}_{2}}$,∴△PF1F2为直角三角形,
又△PF1F2的面积为9,∴$\frac{1}{2}|P{F}_{1}||P{F}_{2}|=9$,得|PF1||PF2|=18.
在Rt△PF1F2中,由勾股定理得:$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}=|{F}_{1}{F}_{2}{|}^{2}$,
∴$(|P{F}_{1}|+|P{F}_{2}|)^{2}-2|P{F}_{1}||P{F}_{2}|=4{c}^{2}$,即2(a2-c2)=|PF1||PF2|=18,
得b2=a2-c2=9,∴b=3.
故选:A.
点评 本题考查椭圆的简单性质,考查了椭圆定义及余弦定理在解焦点三角形问题中的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l∥β,则α∥β | B. | 若l∥α,α∥β,则l∥β | C. | 若l⊥α,l∥β,则α⊥β | D. | 若l⊥α,l⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com