
【题目】在直角坐标系xOy中,已知直线l过点P(2,2).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ﹣ρcos2θ﹣4cosθ=0.
(1)求C的直角坐标方程;
(2)若l与C交于A,B两点,求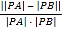 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )

A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF![]() 平面ABCD,DE=DA=DB=2
平面ABCD,DE=DA=DB=2
(I)若G为DC的中点,求证:EG//平面BCF;
(II)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
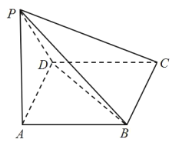
(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
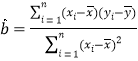
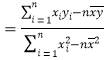 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
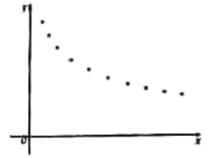
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图).
|
|
|
|
|
|
|
1.63 | 37.8 | 0.89 | 5.15 | 0.92 |
| 18.40 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适合作价格
哪一个更适合作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() ,求该产品投放市场第几天的销售额最高?最高为多少元?
,求该产品投放市场第几天的销售额最高?最高为多少元?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为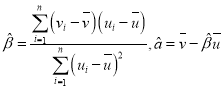 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com