
| m-1 | ||
|
| n-m-1 | ||
|
| 4 |
| m(n-m) |
| 1 | ||
|
| C | 2 m |
| 4 |
| m(n-m) |


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、18焦耳 | B、361焦耳 |
| C、342焦耳 | D、324焦耳 |
查看答案和解析>>
科目:高中数学 来源: 题型:
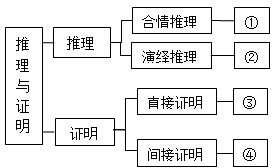 如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )
如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )| A、“①”处 | B、“②”处 |
| C、“③”处 | D、“④”处 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lim |
| h→∞ |
| f(x0+h)-f(x0-h) |
| h |
| A、f′(x0) |
| B、2f′(x0) |
| C、-2f′(x0) |
| D、0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 1 |
| a |
| 1 |
| a |
| A、m<n |
| B、m=n |
| C、m>n |
| D、m,n的大小关系不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com