
| A. | 100 | B. | 88 | C. | 77 | D. | 68 |
分析 根据利用等比数列通项公式及(a1+a4+a7+…+a97)q2=(a2+a5+a6+…+a98)q=a3+a6+a9+…a99求得答案.
解答 解:因为等比数列{an}中,q=2,a2+a5+…+a98=22,
设a3+a6+a9+…+a99=x则
a1+a4+a7+…+a97=$\frac{x}{4}$
a2+a5+a8+…+a98=$\frac{x}{2}$=22,
则x=44,
所以a1+a4+a7+…+a97=11,a3+a6+a9+…+a99=44.
所以S99=(a1+a4+a7+…+a97)+(a2+a5+a6+…+a98)+(a3+a6+a9+…+a99)=44+22+11=77
故选:C.
点评 本题主要考查了等比数列的前n项和,解题的关键是发现a1+a4+a7+…+a97与a2+a5+a6+…+a98和a3+a6+a9+…a99的联系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得f(x0)=0 | |
| B. | 函数y=f(x)的图象一定是中心对称图形 | |
| C. | 若x0是函数f(x)的极值点,则f'(x0)=0 | |
| D. | 若x0是函数f(x)的极小值点,则函数f(x)在区间(-∞,x0)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | m | C. | 2m | D. | 4m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
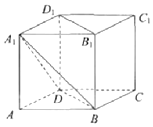 如图,在正方体ABCD-A1B1C1D1中,AB=2,平面α经过B1D1,直线AC1∥α,则平面α截该正方体所得截面的面积为( )
如图,在正方体ABCD-A1B1C1D1中,AB=2,平面α经过B1D1,直线AC1∥α,则平面α截该正方体所得截面的面积为( )| A. | 2$\sqrt{3}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{34}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com