
分析 (Ⅰ)设公比为q,且q>1,由等比数列的通项公式及等差中项的性质,列出方程组求出a1、q,即可求出通项公式;
(Ⅱ)由(Ⅰ)和对数的运算性质化简bn,利用裂项相消法求出前n项和Tn.
解答 解:(Ⅰ)设公比为q,且q>1,
由题意得,$\left\{\begin{array}{l}{{a}_{1}+{a}_{2}+{a}_{3}=7}\\{6{a}_{2}=({a}_{1}+3)+({a}_{3}+4)}\end{array}\right.$,
则$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}=7}\\{6{a}_{1}q={a}_{1}+{a}_{1}{q}^{2}+7}\end{array}\right.$,解得解得a1=1,q=2,
所以an=2n-1;(6分)
(Ⅱ)由(Ⅰ)得 ${{a}_{n}}={{2}^{n-1}}$,
则log2an+1=n,log2an+1+1=n+1,
所以${b}_{n}=\frac{1}{({log}_{2}{a}_{n}+1)({log}_{2}{a}_{n+1}+1)}$
=$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,
则Tn=b1+b2+…+bn
=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n}-\frac{1}{n+1})$
=$1-\frac{1}{n+1}$=$\frac{n}{n+1}$ (12分)
点评 本题考查了等比数列的通项公式,等差中项的性质,以及数列求和方法:裂项相消法,考查方程思想,化简、变形能力.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
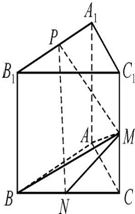 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N,P分别是CC1,BC,A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N,P分别是CC1,BC,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com