
分析 (1)由等比数列的通项公式列出方程组,求出a1、q,即可求出通项公式;
(2)由(1)和对数的运算性质化简bn,利用错位相减法求出数列$\left\{{\frac{b_n}{a_n}}\right\}$的前n项和Tn.
解答 解:(1)由题意得$\left\{\begin{array}{l}{a_1}q+{a_1}{q^2}=12\\{a_1}{q^3}=16\end{array}\right.$,即$\left\{\begin{array}{l}{{a}_{1}q(1+q)=12}\\{{a}_{1}q•{q}^{2}=16}\end{array}\right.$,
两式相除得,$\frac{q^2}{1+q}=\frac{4}{3}$,即3q2-4q-4=0,
又q>0,得q=2,代入得a1=2,
所以${a_n}={2^n}$;
(2)由(1)得${b_n}={log_2}{2^n}=n,\frac{b_n}{a_n}=\frac{n}{2^n}$,
所以${T_n}=\frac{1}{2^1}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n}{2^n}$①,
$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+…+\frac{n-1}{2^n}+\frac{n}{{{2^{n+1}}}}$②
由①-②得,$\frac{1}{2}{T}_{n}=\frac{1}{{2}^{1}}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$
=$\frac{\frac{1}{2}[1-{(\frac{1}{2})}^{n}]}{1-\frac{1}{2}}-\frac{n}{{2}^{n+1}}=1-\frac{n+2}{{2}^{n+1}}$,
所以Tn=$2-\frac{n+2}{{2}^{n}}$.
点评 本题考查了等比数列的通项公式,以及数列求和方法:错位相消法,考查方程思想,化简、变形能力.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p一定是真命题 | B. | 命题q一定是真命题 | ||
| C. | 命题q一定是假命题 | D. | 命题p也可以是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得f(x0)=0 | |
| B. | 函数y=f(x)的图象一定是中心对称图形 | |
| C. | 若x0是函数f(x)的极值点,则f'(x0)=0 | |
| D. | 若x0是函数f(x)的极小值点,则函数f(x)在区间(-∞,x0)上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
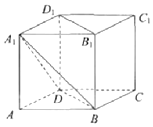 如图,在正方体ABCD-A1B1C1D1中,AB=2,平面α经过B1D1,直线AC1∥α,则平面α截该正方体所得截面的面积为( )
如图,在正方体ABCD-A1B1C1D1中,AB=2,平面α经过B1D1,直线AC1∥α,则平面α截该正方体所得截面的面积为( )| A. | 2$\sqrt{3}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{34}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com