
【题目】已知函数f(x)=x2+2ax+a2﹣1.
(1)若对任意的x∈R均有f(1﹣x)=f(1+x),求实数a的值;
(2)当x∈[﹣1,1]时,求f(x)的最小值,用g(a)表示其最小值,判断g(a)的奇偶性.
【答案】
(1)解:∵函数f(x)=x2+2ax+a2﹣1对任意的实数x都有f(1+x)=f(1﹣x)成立,
∴函数的对称轴x=﹣a=1,
∴a=﹣1
(2)解:∵f(x)=x2+2ax+a2﹣1=(x+a)2﹣1,其对称轴为x=﹣a,
当﹣a≤﹣1时,即a≥1时,函数f(x)在[﹣1,1]上单调递增,故g(a)=f(x)min=f(﹣1)=a2﹣2a,
当﹣1<﹣a<1时,即﹣1<a<1时,故g(a)=f(x)min=f(a)=﹣1,
当﹣a≥1时,即a≤﹣1时,函数f(x)在[﹣1,1]上单调递减,故g(a)=f(x)min=f(1)=a2+2a,
∴g(a)= 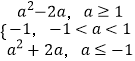 ,
,
∵g(﹣a)=g(a),
∴g(a)为偶函数
【解析】1、由二次函数的性质可得对任意的实数x都有f(1+x)=f(1﹣x)成立,函数的对称轴x=﹣a=1,∴a=﹣1。
2、由二次函数的图象和性质,当﹣a≤﹣1时,即a≥1时,函数f(x)在[﹣1,1]上单调递增,故g(a)=f(x)min=f(﹣1)=a2﹣2a
当﹣1<﹣a<1时,即﹣1<a<1时,故g(a)=f(x)min=f(a)=﹣1,当﹣a≥1时,即a≤﹣1时,函数f(x)在[﹣1,1]上单调递减,故g(a)=f(x)min=f(1)=a2+2a,得出函数的解析式,由偶函数定义可证。
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 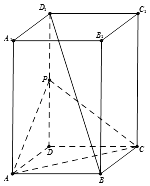
(1)求证:直线BD1∥平面PAC
(2)求证:平面PAC⊥平面BDD1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x∈[0,+∞)时,f(x)=2x+x﹣m(m为常数).
(1)求常数m的值.
(2)求f(x)的解析式.
(3)若对于任意x∈[﹣3,﹣2],都有f(k4x)+f(1﹣2x+1)>0成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=logax在区间(0,+∞)上是单调递增函数;命题q:不等式(a﹣2)x2+2(a﹣2)x﹣4<0对任意实数x恒成立.若p∨q为真命题,且p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() .
.
(1)利用定义证明:函数f(x)在区间(0,+∞)上为增函数;
(2)当x∈(0,1)时,tf(2x)≥2x﹣1恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O为Rt△ABC的外接圆,AB=AC,BC=4,过圆心O的直线l交圆O于P,Q两点,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣8,﹣1]
B.[﹣8,0]
C.[﹣16,﹣1]
D.[﹣16,0]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点. 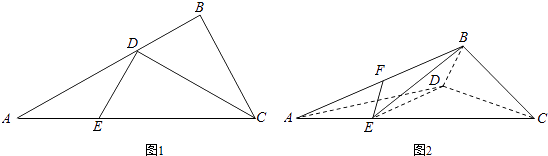
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B﹣DEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,给出下面四个命题,则其中正确命题的个数为( )
①过平面 ![]() 外的两点,有且只有一个 平面与平面
外的两点,有且只有一个 平面与平面 ![]() 垂直;
垂直;
②若平面 ![]() 内有不共线三点到平面
内有不共线三点到平面 ![]() 的距离都相等,则
的距离都相等,则 ![]() ∥
∥ ![]() ;
;
③若直线 ![]() 与平面内的无数条直线垂直,则
与平面内的无数条直线垂直,则 ![]() ;
;
④两条异面直线在同一平面内的射影一定是两平行线;
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com