
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.
(1)求证:平面ABM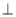 平面PCD;
平面PCD;
(2)求三棱锥M-ABD的体积.

(1)见解析(2)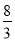
【解析】
试题分析:(1)由PA⊥平面ABCD知,PA⊥AB,由ABCD为矩形知,AB⊥AD,由线面垂直判定定理知,AB⊥PAD,所以PB⊥AB,由以BD为直径的球与PB的交点为M知,BM⊥DM,由线面垂直判定知PD⊥面ABM,由面面垂直判定定理知面PCD⊥面ABM;(2)由(1)知,PD⊥面ABM,所以PD⊥AM,因为PA=AD=4,所以M是PD的中点,取AD的中点为N,则NM平行PA,因为PA⊥平面ABCD,所以MN⊥ABCD,MN=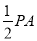 =2,即MN是三棱锥M-ABD的高,用棱锥的体积公式即可求出其体积.
=2,即MN是三棱锥M-ABD的高,用棱锥的体积公式即可求出其体积.
试题解析:(1)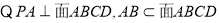
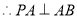
又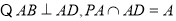
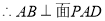
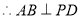
由题意得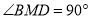 ,
,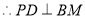
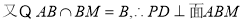
又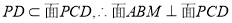 6分
6分
(2)由(1)知,PD⊥面ABM,所以PD⊥AM,
因为PA=AD=4,所以M是PD的中点,
取AD的中点为N,则NM平行PA,
因为PA⊥平面ABCD,所以MN⊥ABCD,MN=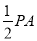 =2,
=2,
所以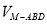 =
=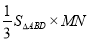 =
=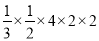 =
=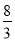 . 12分
. 12分
考点:球的性质,线面垂直的判定与性质,面面垂直判定定理,棱锥的体积公式,逻辑推论证能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
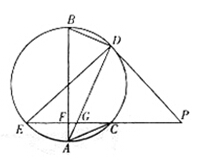
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证: .
.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
函数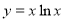 的单调递减区间是( ).
的单调递减区间是( ).
A、(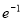 ,+∞) B、(-∞,
,+∞) B、(-∞,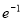 ) C、(0,
) C、(0,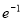 ) D、(e,+∞)
) D、(e,+∞)
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
若点P是曲线y=x2-ln x上任意一点,则点P到直线y=x-2的最小值为( )
A.1 B.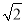 C.
C. D.
D.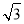
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知命题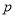 :“
:“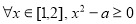 ”,命题
”,命题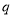 :“
:“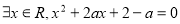 ”.
”.
若命题“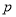 且
且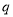 ”是真命题,则实数
”是真命题,则实数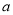 的取值范围为( )
的取值范围为( )
A. 或
或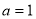 B.
B. 或
或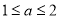
C.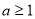 D.
D.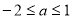
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知函数 的图象在点(-1,2)处的切线恰好与直线3x+y=0平行,若
的图象在点(-1,2)处的切线恰好与直线3x+y=0平行,若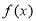 在区间
在区间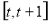 上单调递减,则实数t的取值范围是_____________
上单调递减,则实数t的取值范围是_____________
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
下面框图所给的程序运行结果为S=28,那么判断框中应填入的关于k的条件是( )
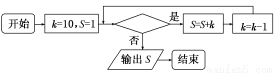
A. ? B.k≤7? C.k<7? D.k>7?
? B.k≤7? C.k<7? D.k>7?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com