
如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
(1)求证:AB为圆的直径;
(2)若AC=BD,求证: .
.
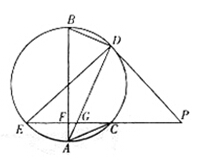
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:
解题思路:(1)利用直径所对的圆周角为直角,证明 即可;(2)利用全等三角形即(1)结论证明
即可;(2)利用全等三角形即(1)结论证明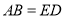 .
.
规律总结:本题考查几何证明中的直线与圆的位置关系,培养学生的观察能力以及分析问题的能力.
试题解析:(1)因为PD=PG,所以∠PDG=∠PGD.
由于PD为切线,故∠PDA=∠DBA,又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.
由于AF垂直EP,所以∠PFA=90°,于是∠BDA=90°,故AB是直径.
(2)连接BC,DC.
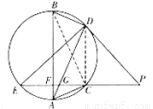
由于AB是直径,故∠BDA=∠ACB=90°,
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,
从而Rt△BDA≌Rt△ACB,于是∠DAB=∠CBA.
又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.
由于
于是ED是直径,由(1)得ED=AB.
考点:直线与圆的位置关系.


科目:高中数学 来源:2015数学一轮复习迎战高考:10-2排列与组合(解析版) 题型:填空题
[2014·南京模拟]用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有________个.(用数字作答)
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考10-1分类加法计数原理与分步乘法计数原理(解析版) 题型:选择题
[2014·北京模拟]如图,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂1种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有( )
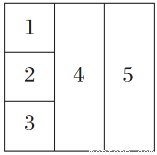
A.72种 B.96种 C.108种 D.120种
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考1-3简单逻辑联结词、全称量词与存在量词(解析版) 题型:选择题
已知命题p:?x∈R,mx2+1≤0,命题q:?x∈R,x2+mx+1>0,若p∧q为真命题,则实数m的取值范围是( )
A.(-∞,-2) B.[-2,0)
C.(-2,0) D.(0,2)
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知向量 ,n∈N*,向量
,n∈N*,向量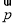 与
与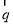 垂直,且a1=1.
垂直,且a1=1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知点P(x,y)在不等式组 表示的平面区域上运动,则x-y的取值范围是( ).
表示的平面区域上运动,则x-y的取值范围是( ).
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
在△ABC中,设A、B、C的对边分别为a、b、c,向量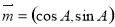 ,
,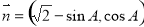 ,若
,若
(1)求角A的大小;
(2)若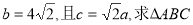 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,以BD的中点O为球心、BD为直径的球面交PD于点M.
(1)求证:平面ABM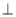 平面PCD;
平面PCD;
(2)求三棱锥M-ABD的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com