
(2014•唐山二模)用简单随机抽样的方法从含有100个个体的总体中依次抽取一个容量为5的样本,则个体m被抽到的概率为( )
A.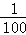 B.
B.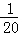 C.
C.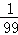 D.
D.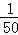
科目:高中数学 来源:[同步]2014年北师大版必修三 1.6统计活动:结婚年龄的变化练习卷(解析版) 题型:选择题
(2014•雅安三模)某班有男生36人,女生18人,用分层抽样的方法从该班全体学生中抽取一个容量为6的样本,则抽取的女生人数为( )
A.6 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版必修三 1.1从普查到抽样练习卷(解析版) 题型:选择题
在某学校组织的一次数学模拟考试成绩统计中,工作人员采用简单随机抽样的方法,抽取一个容量为50的样本进行统计,若每个学生的成绩被抽到的概率为0.1,则可知这个学校参加这次数学考试的人数是( )
A.100人 B.600人 C.225人 D.500人
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版必修三 1.1从普查到抽样练习卷(解析版) 题型:选择题
现有以下两项调查:①某校高二年级共有15个班,现从中选择2个班,检查其清洁卫生状况;②某市有大型、中型与小型的商店共1500家,三者数量之比为1:5:9.为了调查全市商店每日零售额情况,抽取其中15家进行调查.完成①、②这两项调查宜采用的抽样方法依次是( )
A.简单随机抽样法,分层抽样法
B.系统抽样法,简单随机抽样法
C.分层抽样法,系统抽样法
D.系统抽样法,分层抽样法
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教B版选修2-1 第二章 圆锥曲线与方程练习卷(解析版) 题型:解答题
(12分)已知椭圆C1: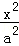 +
+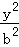 =1(0<a<
=1(0<a<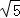 ,0<b<2)与椭圆C2:
,0<b<2)与椭圆C2: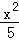 +
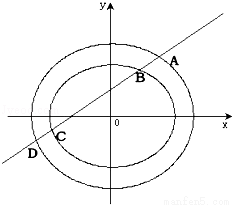
+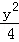 =1有相同的焦点.直线L:y=k(x+1)与两个椭圆的四个交点,自上而下顺次记为A、B、C、D.
=1有相同的焦点.直线L:y=k(x+1)与两个椭圆的四个交点,自上而下顺次记为A、B、C、D.
(Ⅰ)求线段BC的长(用k和a表示);
(Ⅱ)是否存在这样的直线L,使线段AB、BC、CD的长按此顺序构成一个等差数列.请说明详细的理由.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教B版选修2-1 第二章 圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)已知双曲线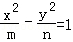 (mn≠0)的离心率为2,有一个焦点恰好是抛物线y2=4x的焦点,则此双曲线的渐近线方程是( )
(mn≠0)的离心率为2,有一个焦点恰好是抛物线y2=4x的焦点,则此双曲线的渐近线方程是( )
A.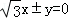 B.
B.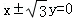 C.3x±y=0 D.x±3y=0
C.3x±y=0 D.x±3y=0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.4练习卷(解析版) 题型:填空题
(2014•郴州二模)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:填空题
(2011•宝山区二模)如图,在梯形ABCD中,AD∥BC,AC、BD相交于O,记△BCO、△CDO、△ADO的面积分别为S1、S2、S3,则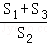 的取值范围是 .
的取值范围是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com