
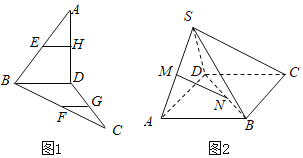
【题目】(1)如图(1)已知E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH![]() FG.求证:EH
FG.求证:EH![]() BD.
BD.
(2)如图(2):S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且![]() ,求证:MN
,求证:MN![]() 平面SBC.
平面SBC.
【答案】(1)见解析 (2)见解析
【解析】
(1)先证明EH![]() 平面BCD,再利用线面平行的性质即可得证;
平面BCD,再利用线面平行的性质即可得证;
(2)过N作NG![]() AD,交AB于G,证明MG
AD,交AB于G,证明MG![]() 平面SBC、NG
平面SBC、NG![]() 平面SBC后即可证明平面SBC
平面SBC后即可证明平面SBC![]() 平面MNG,即可得证.
平面MNG,即可得证.
(1)证明:如图(1),E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,
∵EH![]() FG,EH平面BCD,FG平面BCD,
FG,EH平面BCD,FG平面BCD,
∴EH![]() 平面BCD,
平面BCD,
∵平面ABD∩平面BCD=BD,∴BD平面ABD,
∵EH平面ABD,∴EH![]() BD.
BD.
(2)证明:如图(2),S是平行四边形ABCD平面外一点,
过N作NG![]() AD,交AB于G,连接MG,可得
AD,交AB于G,连接MG,可得![]() ,
,
由已知条件![]() ,得
,得![]() ,∴MG
,∴MG![]() SB.
SB.
∵MG平面SBC,SB平面SBC,∴MG![]() 平面SBC.
平面SBC.
又AD![]() BC,∴NG
BC,∴NG![]() BC,
BC,
∵NG平面SBC,BC平面SBC
∴NG![]() 平面SBC,NG∩MG=G,
平面SBC,NG∩MG=G,
∴平面SBC![]() 平面MNG,
平面MNG,
∵MN平面MNG,∴MN![]() 平面SBC.
平面SBC.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,点
,点![]() 为短轴的一个端点,
为短轴的一个端点,![]() .
.
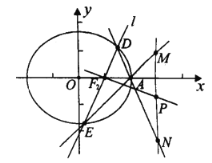
(1)求椭圆C的方程;
(2)如图,过右焦点![]() ,且斜率为k(
,且斜率为k(![]() )的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线
)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点M,N,线段
于点M,N,线段![]() 的中点为P,记直线
的中点为P,记直线![]() 的斜率为
的斜率为![]() .试问
.试问![]() 是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线过点
,抛物线过点![]() .
.
(Ⅰ)求抛物线![]() 的标准方程与其准线
的标准方程与其准线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线与抛物线
点作直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线的切线,证明两条切线的交点在抛物线
分别作抛物线的切线,证明两条切线的交点在抛物线![]() 的准线
的准线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点外卖现已成为上班族解决午餐问题的一种流行趋势.某配餐店为扩大品牌影响力,决定对新顾客实行让利促销,规定:凡点餐的新顾客均可获赠10元或者16元代金券一张,中奖率分别为![]() 和
和![]() ,每人限点一餐,且100%中奖.现有A公司甲、乙、丙、丁四位员工决定点餐试吃.
,每人限点一餐,且100%中奖.现有A公司甲、乙、丙、丁四位员工决定点餐试吃.
(Ⅰ) 求这四人中至多一人抽到16元代金券的概率;
(Ⅱ) 这四人中抽到10元、16元代金券的人数分别用![]() 、
、![]() 表示,记
表示,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com