Question

（09年临沭县模块考试文）（12分）

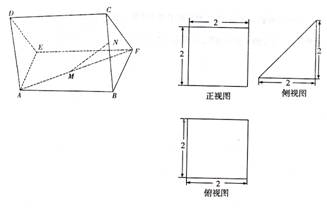
       多面体AEDBFC的直观图及三视图如图所示，MN分别为AF，BC的中点。

   （Ⅰ）求证MN∥平面CDEF；

   （Ⅱ）求多面体A―CDEF的体积。

Answer 1

解析：

   （Ⅰ）由多面体AEBFC的三视图可知

       三棱柱AED―BFC中，底面DAE是等腰直角三角形，

       DA=AE=2，DA⊥平面ABFE，                                                  ????????????????1分

       侧面ABFE，ABCD都是边长为2的正方形                               ????????????????3分

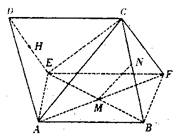
   （Ⅰ）连EB，CE，∴M是EB中点，

       又∵N是BC中点，在△BEC中，MN∥EC                                ????????????????5分

       又∵EC平面CDEF，MN平面CDEF，∴MN∥平面CDEF。???????????????6分

   （Ⅱ）∵DA⊥平面ABEF，EC平面ABEF，∴AD⊥EF，

       又∵EF⊥AE，∴EF⊥平面AED，∴四边形CDEF是矩形，侧面CDEF⊥平面AED

                                                                                                      ????????????????8分

       取DE中点H，∵△AED为等腰直角三角形，且AD=AE=2，

       ∴AH⊥DE，且AH=

       ∴AH⊥平面CDEF                                                                   ?????????????????11分

       ∴

                                                                ?????????????????12分