
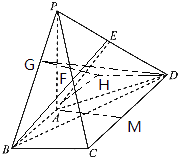
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD= ![]() ,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点. 
(1)求证:AE∥平面PBC;
(2)若直线AE与直线BC所成角等于 ![]() ,求二面角D﹣PB﹣A平面角的余弦值.
,求二面角D﹣PB﹣A平面角的余弦值.
【答案】
(1)证明:取PC中点F,连结EF、BF,
∴△PCD中,EF ![]()
![]() ,AB
,AB ![]()
![]() ,
,
∴EF ![]() AB,
AB,
∴四边形ABFE为平行四边形,
∵AE∥BF,AE平面PBC,BF平面PBC,
∴AE∥平面PBC.
(2)解:AE与直线BC所成角为 ![]() ,
, ![]() ,
,
∴BP= ![]() ,∴PA=
,∴PA= ![]() ,
,
延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,
则∠DGH是二面角D﹣PB﹣A的平面角,
DH=1,FG× ![]() ,HG=
,HG= ![]() ,
,
∴tan∠DGH= ![]() ,
,
∴cos∠DGH= ![]()
![]() .
.
∴二面角D﹣PB﹣A平面角的余弦值为 ![]() .
.
【解析】(1)取PC中点F,连结EF、BF,推导出四边形ABFE为平行四边形,从而AE∥BF,由此能证明AE∥平面PBC.(2)AE与直线BC所成角为 ![]() ,延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,∠DGH是二面角D﹣PB﹣A的平面角,由此能求出二面角D﹣PB﹣A平面角的余弦值.
,延长BA一倍到H,连结DH,再作HG⊥BP,连结DG,∠DGH是二面角D﹣PB﹣A的平面角,由此能求出二面角D﹣PB﹣A平面角的余弦值.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:

(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在班级活动中,4名男生和3名女生站成一排表演节目:(写出必要的数学式,结果用数字作答)
(1)三名女生不能相邻,有多少种不同的站法?
(2)四名男生相邻有多少种不同的排法?
(3)女生甲不能站在左端,女生乙不能站在右端,有多少种不同的排法?
(4)甲乙丙三人按高低从左到右有多少种不同的排法?(甲乙丙三位同学身高互不相等)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)经过点P(﹣2,0)与点(1,1).
=1(a>b>0)经过点P(﹣2,0)与点(1,1).
(1)求椭圆的方程;
(2)过P点作两条互相垂直的直线PA,PB,交椭圆于A,B.
①证明直线AB经过定点;
②求△ABP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y满足约束条件  ,目标函数z=ax+by(a>0,b>0)的最大值M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积= .
,目标函数z=ax+by(a>0,b>0)的最大值M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinωxcosωx+2 ![]() sin2ωx﹣
sin2ωx﹣ ![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移 ![]() 个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在
个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象,求函数y=g(x)在 ![]() 上的最值.
上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)解不等式: ![]()
(2)有4名男生和3名女生
i)选出4人去参加座谈会,如果3人中必须既有男生又有女生,有多少种选法?
ii)7人排成一排,甲乙二人之间恰好有2个人,有多少种不同的排法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com