练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在（1+x）6（1+y）4的展开式中，记xmyn项的系数为f（m，n），则f（2，1）+f（1，2）=（　　）
    A、45B、60C、96D、108
    考点：二项式系数的性质
    专题：二项式定理
    分析：按照二项式定理把（1+x）6（1+y）4展开，求得f（2，1）和f（1，2）的值，可得f（2，1）+f（1，2）的值．
    解答： 解：（1+x）6（1+y）4 =（1+6x+15x2+20x3+15x4+6x5+x6） （1+4y+6y2+4y3+y4），
    ∴f（2，1）=15×4=60，f（1，2）=6×6=36，∴f（2，1）+f（1，2）=96，
    故选：C．
    点评：本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知抛物线y2=4x，点M（1，0）关于y轴的对称点为N，直线l过点M交抛物线于A，B两点，
    （1）证明：直线NA，NB的斜率互为相反数；
    （2）求△ANB面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，一小山峰BC的高为30cm，山顶上有建筑物CD的高为20cm，建筑物上竖一高为40m铁架DE，问在底面上距离B多远的地方，能找到这样一点A，使得∠BAC=∠DAE？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    F是抛物线y2=2px（p＞0）的焦点，P是抛物线上一点，FP延长线交y轴于Q，若P恰好是FQ的中点，则|PF|=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x|-1＜x＜6}，B={x|-9＜x＜
    3
    2
    }，C={x|1-2a＜x＜2a}．
    （1）若C=∅，求实数a的取值范围；
    （2）若C≠∅且C⊆（A∩B），求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为DD1的中点
    （1）求证：BD1∥平面AEC
    （2）求证：平面D1DB⊥平面AEC
    （3）若P为对角线D1B的中点，Q为棱C1C上的动点求|PQ|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

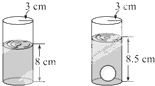    一个圆柱形的玻璃瓶的内半径为3cm，瓶里所装的水深为8cm，将一个钢球完全浸入水中，瓶中水的高度上升到8.5cm，则钢球的半径为（　　）
    A、1 cm
    B、1.2 cm
    C、1.5 cm
    D、2 cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求中心在原点、焦点在坐标轴上，与椭圆4x2+9y2=36有相同的焦点，且离心率为
    		5
    5
    的椭圆方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

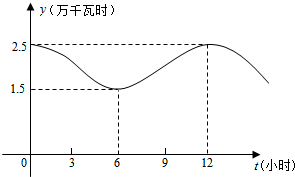    某大型企业一天中不同时刻的用电量y（单位：万千瓦时）关于时间t（0≤t≤24，单位：小时）的函数y=f（t）近似地满足f（t）=Asin（ωt+φ）+B（A＞0，ω＞0，0＜φ＜π），如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象．
    （Ⅰ）根据图象，求A，ω，φ，B的值；
    （Ⅱ）若某日的供电量g（t）（万千瓦时）与时间t（小时）近似满足函数关系式g（t）=-15t+20（0≤t≤12）．当该日内供电量小于该企业的用电量时，企业就必须停产．请用二分法计算该企业当日停产的大致时刻（精确度0.1）．
    参考数据：
    t（时）10111211.511.2511.7511.62511.6875
    f（t）（万千瓦时）2.252.4332.52.482.4622.4962.4902.493
    g（t）（万千瓦时）53.522.753.1252.3752.5632.469

    查看答案和解析>>

    同步练习册答案