
分析 (1)对x讨论,当0<x≤20,x∈N*时,当x>20,x∈N*时,由利润为收入减成本,即可得到f(x)的解析式;
(2)运用二次函数的最值求法和一次函数的单调性,即可得到最大值.
解答 解:(1)当0<x≤20,x∈N*时,f(x)=30x-x2-(80+2x)=-x2+28x-80;
当x>20,x∈N*时,f(x)=210-(80+2x)=-2x+130.
即有f(x)=$\left\{\begin{array}{l}{-{x}^{2}+28x-80,0<x≤20,x∈N}\\{-2x+130,x>20,x∈N}\end{array}\right.$;
(2)当0<x≤20,x∈N*时,f(x)=-(x-14)2+116,
当x=14时,f(x)取得最大值116;
当x>20时,f(x)递减,即f(x)<90.
则当年产量为14件时,所得年利润最大,且为116万元.
点评 本题考查分段函数的运用,考查函数的最值的求法,注意运用二次函数和一次函数的单调性,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
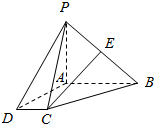 如图,四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2n-1 | C. | n2 | D. | 2n2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com