考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)要证面面垂直,需证线面垂直,根据已知,需证AB1⊥面B1CD,然后需证AB1⊥CD,然后再证CD⊥面AB1D,根据面面垂直的性质,不难证明,则将以上过程逆回去,即可证明结论;
(2)根据体积公式,由已知,容易求得△ABC的面积,而高即为B1O,又易证△AB1D为直角△,则斜边AD上的高B1O可求,则体积VB1-ABC-ABC迎刃而解.
解答:
解:(1)∵B
1O⊥平面ABCD,CD?平面ABCD,
∴B
1O⊥CD,又CD⊥AD,AD∩B
1O=O
∴CD⊥平面AB
1D,又AB
1?平面AB
1D
∴AB
1⊥CD,又AB
1⊥B
1C,且B
1C∩CD=C
∴AB
1⊥平面B
1CD,又AB
1?平面AB
1C
∴平面AB
1C⊥平面B
1CD.
(2)由于AB
1⊥平面B
1CD,B
1D?平面ABCD,
所以AB
1⊥B
1D
在Rt△AB
1D中,
B1D==,
又由B
1O•AD=AB
1•B
1D得
B1O==
,
所以
VB1-ABC=S△ABC•B1O=××1××=.
点评:线面的平行、垂直的证明,主要是线线、线面、面面三者之间的平行间关系的转化,垂直间关系的转化,或平行与垂直间的转化,充分体现了转化与化归思想的应用;三棱锥的体积问题,关键是选好底面与高,一般需要变换一下底面与顶点.

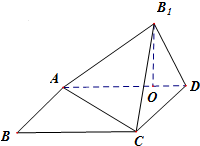 已知四边形ABCD是矩形,AB=1,BC=
已知四边形ABCD是矩形,AB=1,BC=

 阅读快车系列答案
阅读快车系列答案