
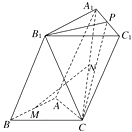
【题目】如图,已知三棱柱 ![]() ,侧面
,侧面 ![]() .
.
(Ⅰ)若 ![]() 分别是
分别是 ![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若三棱柱 ![]() 的各棱长均为2,侧棱
的各棱长均为2,侧棱 ![]() 与底面
与底面 ![]() 所成的角为
所成的角为 ![]() ,问在线段
,问在线段 ![]() 上是否存在一点
上是否存在一点 ![]() ,使得平面
,使得平面 ![]() ?若存在,求
?若存在,求 ![]() 与
与 ![]() 的比值,若不存在,说明理由.
的比值,若不存在,说明理由.
【答案】解:证明:(Ⅰ)连接AC1 , BC1 , 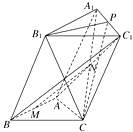
则AC1∩A1C=N,AN=NC1 ,
因为AM=MB,所以MN∥BC1.
又BC1平面BCC1B1 ,
所以MN∥平面BCC1B1.
(Ⅱ)作B1O⊥BC于O点,连接AO,
因为平面BCC1B1⊥底面ABC,
所以B1O⊥平面ABC,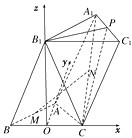
以O为原点,建立如图所示的空间直角坐标系,则A(0, ![]() ,0),B(-1,0,0),C(1,0,0),B1(0,0,
,0),B(-1,0,0),C(1,0,0),B1(0,0, ![]() ).由
).由 ![]() =
= ![]() =
= ![]() ,可求出A1(1,
,可求出A1(1, ![]() ,
, ![]() ),C1(2,0,
),C1(2,0, ![]() ),
),
设点P(x,y,z), ![]() =λ
=λ ![]() .
.
则P ![]() ,
,![]() =
= ![]() ,
,![]() =(-1,0,
=(-1,0, ![]() ).
).
设平面B1CP的法向量为n1=(x1 , y1 , z1),
由 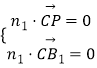
得 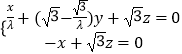
令z1=1,解得n1= ![]() .
.
同理可求出平面ACC1A1的法向量n2=( ![]() ,1,-1).
,1,-1).
由平面B1CP⊥平面ACC1A1 ,
得n1·n2=0,即3+ ![]() -1=0,
-1=0,
解得λ=3,所以A1C
从而C1P∶PA1=2.
【解析】(1)连接AC1,利用三角形的中位线证明:MN∥BC1,然后利用直线与平面平行的判定定理证明即可.
(2)假设在线段A1C1上存在点P,通过求出平面B1CP的法向量,求出平面ACC1A1的法向量,通过向量垂直的条件建立方程.即可得出结论.
【考点精析】认真审题,首先需要了解平面的法向量(若向量![]() 所在直线垂直于平面
所在直线垂直于平面![]() ,则称这个向量垂直于平面
,则称这个向量垂直于平面![]() ,记作
,记作![]() ,如果
,如果![]() ,那么向量
,那么向量![]() 叫做平面
叫做平面![]() 的法向量).
的法向量).


科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(Ⅰ)证明:不论t为何值,直线l与曲线C恒有两个公共点;
(Ⅱ)以α为参数,求直线l与曲线C相交所得弦AB的中点轨迹的参数方程,并判断该轨迹的曲线类型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市![]() 岁的人群抽取一个容量为
岁的人群抽取一个容量为![]() 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
,再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样方法抽取
组回答正确的人中用分层抽样方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求:所抽取的人中第2组至少有
人颁发幸运奖,求:所抽取的人中第2组至少有![]() 人获得幸运奖概率.
人获得幸运奖概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(sinx+cosx).
(1)如果对于任意的x∈[0, ![]() ],f(x)≥kx+excosx恒成立,求实数k的取值范围;
],f(x)≥kx+excosx恒成立,求实数k的取值范围;
(2)若x∈[﹣ ![]() ,
, ![]() ],过点M(
],过点M( ![]() ,0)作函数f(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{xn},求数列{xn}的所有项之和.
,0)作函数f(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{xn},求数列{xn}的所有项之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() ,过点
,过点 ![]() 的直线
的直线 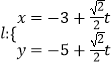 (
( ![]() 为参数)与曲线
为参数)与曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() 两点.
两点.
(1)求曲线 ![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线 ![]() 的普通方程;
的普通方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
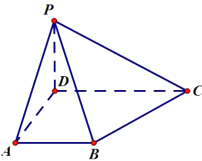
【题目】如图,四棱锥 ![]() 中,底面
中,底面 ![]() 为梯形,
为梯形, ![]() 底面
底面 ![]() ,
, ![]() .过
.过 ![]() 作一个平面
作一个平面 ![]() 使得
使得 ![]() 平面
平面 ![]() .
.
(1)求平面 ![]() 将四棱锥
将四棱锥 ![]() 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;
(2)若平面 ![]() 与平面
与平面 ![]() 之间的距离为
之间的距离为 ![]() ,求直线
,求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com