
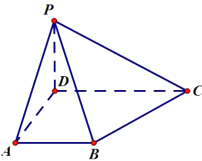
【题目】如图,四棱锥 ![]() 中,底面
中,底面 ![]() 为梯形,
为梯形, ![]() 底面
底面 ![]() ,
, ![]() .过
.过 ![]() 作一个平面
作一个平面 ![]() 使得
使得 ![]() 平面
平面 ![]() .
.
(1)求平面 ![]() 将四棱锥
将四棱锥 ![]() 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;
(2)若平面 ![]() 与平面
与平面 ![]() 之间的距离为
之间的距离为 ![]() ,求直线
,求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】
(1)解:记平面 ![]() 与直线
与直线 ![]() .
.
因为 ![]() ,所以
,所以 ![]() .
.
由已知条件易知 ![]() ,又因
,又因 ![]() .
.
所以 ![]()
可得 ![]()
所以 ![]() .
.
即平面 ![]() 将四棱锥
将四棱锥 ![]() 分成两部分几何体的体积之比为
分成两部分几何体的体积之比为 ![]()
(2)解:建立直角坐标系,记 ![]()
则 ![]()
因为平面 ![]() 的法向量
的法向量 ![]()
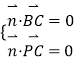
![]()
设 ![]()
![]() 得
得 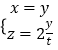 ,
,
取 ![]() 得平面
得平面 ![]() .
.
由条件易知点 ![]() 到平面
到平面 ![]() 距离
距离 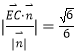 .即
.即 ![]() .
.
所以.直线 ![]() 与平面
与平面 ![]() 所成角
所成角 ![]() 满足
满足 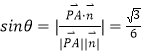
【解析】(Ⅰ)利用线面的垂直,进一步算出锥体的体积运算求出比值.
(Ⅱ)建立直角坐标系,通过做出直线 P A 与平面 P B C 所成角,求出相关的量,进一步求得结果.
【考点精析】关于本题考查的用空间向量求直线与平面的夹角,需要了解设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
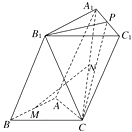
【题目】如图,已知三棱柱 ![]() ,侧面
,侧面 ![]() .
.
(Ⅰ)若 ![]() 分别是
分别是 ![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若三棱柱 ![]() 的各棱长均为2,侧棱
的各棱长均为2,侧棱 ![]() 与底面
与底面 ![]() 所成的角为
所成的角为 ![]() ,问在线段
,问在线段 ![]() 上是否存在一点
上是否存在一点 ![]() ,使得平面
,使得平面 ![]() ?若存在,求
?若存在,求 ![]() 与
与 ![]() 的比值,若不存在,说明理由.
的比值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,.
,.![]()
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.
(Ⅰ) 若BC1∥平面A1CD,确定D的位置,并说明理由;
(Ⅱ) 在(Ⅰ)的条件下,求二面角A1D﹣C﹣BC1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx﹣
sinωx﹣ ![]() cosωx(ω<0),若y=f(x+
cosωx(ω<0),若y=f(x+ ![]() )的图象与y=f(x﹣
)的图象与y=f(x﹣ ![]() )的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣
)的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣ ![]() )的单调递增区间为( )
)的单调递增区间为( )
A.[﹣ ![]() π+
π+ ![]() ,﹣
,﹣ ![]() +
+ ![]() ](k∈Z)
](k∈Z)
B.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
C.[﹣ ![]() π+2kπ,﹣
π+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
D.[﹣ ![]() +2kπ,﹣
+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com