练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知 ，设命题 ：指数函数 ≠ 在 上单调递增.命题 ：函数 的定义域为 ．若“ ”为假，“ ”为真，求 的取值范围．

    【答案】解：由命题p ， 得a＞1，对于命题q ， 即使得x∈R ， ax2－ax＋1＞0恒成立
    若a＞0，△＝a2－4a＜0，即0＜a＜4
    若a＝0，1＞0恒成立，满足题意，所以0≤a＜4
    由题意知p与q一真一假，
    当p真q假时 ， 所以a≥4．
    当p假q真时，， 即0≤a≤1．
    综上可知，a的取值范围为[0，1]∪[4，＋∞)
    【解析】若“p且q”为假，“p或q”为真，则p与q一真一假，进而可得a的取值范围．判断含有“或”、“且”、“非”的复合命题的真假，首先要明确p、q及非p的真假，然后由真值表判断复合命题的真假．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥 中，底面 为菱形，且直线 又棱 为 的中点，
    (Ⅰ) 求证：直线 ；
    (Ⅱ) 求直线 与平面 的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下关于命题的说法正确的有（填写所有正确命题的序号）．
    ①“若 ，则函数 （ ，且 ）在其定义域内是减函数”是真命题；
    ②命题“若 ，则 ”的否命题是“若 ，则 ”；
    ③命题“若 ， 都是偶数，则 也是偶数”的逆命题为真命题；
    ④命题“若 ，则 ”与命题“若 ，则 ”等价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， ，其中 ．
    （1）当 时，求函数 的单调递减区间；
    （2）若对任意的 ， （ 为自然对数的底数）都有 成立，求实数 的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是东西方向的公路北侧的边缘线，某公司准备在上的一点的正北方向的处建一仓库，并在公路同侧建造一个正方形无顶中转站（其中边在上），现从仓库向和中转站分别修两条道路，，已知，且，设，．

    （1）求关于的函数解析式；

    （2）如果中转站四周围墙（即正方形周长）造价为万元，两条道路造价为万元，问：取何值时，该公司建中转围墙和两条道路总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥 中，底面 为梯形， 底面 ， .过 作一个平面 使得 平面 .

    （1）求平面 将四棱锥 分成两部分几何体的体积之比；
    （2）若平面 与平面 之间的距离为 ，求直线 与平面 所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平行四边形 的三个顶点坐标为 ， ， .
    （Ⅰ）求顶点 的坐标；
    （Ⅱ）求四边形 的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

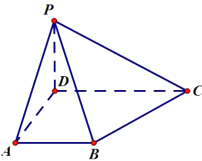
    如图，在四棱锥P—ABCD中，侧面PAD⊥底面ABCD，侧棱PA＝PD=,底面ABCD为直角梯形，其中BC∥AD,AB⊥AD,AD=2AB=2BC=2，O为AD中点.

    (Ⅰ)求证:PO⊥平面ABCD；

    (Ⅱ)求异面直线PB与CD所成角的余弦值；

    (Ⅲ)求点A到平面PCD的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆 的方程为 ，直线 的方程为 ，点 在直线 上，过点 作圆 的切线 ，切点为 .
    （1）若点 的坐标为 ，求切线 的方程；
    （2）求四边形 面积的最小值；
    （3）求证：经过 三点的圆必过定点，并求出所有定点坐标.

    查看答案和解析>>

    同步练习册答案