
【题目】已知圆 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的方程为
的方程为 ![]() ,点
,点 ![]() 在直线
在直线 ![]() 上,过点
上,过点 ![]() 作圆
作圆 ![]() 的切线
的切线 ![]() ,切点为
,切点为 ![]() .
.
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求切线
,求切线 ![]() 的方程;
的方程;
(2)求四边形 ![]() 面积的最小值;
面积的最小值;
(3)求证:经过 ![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
【答案】
(1)解:①当切线斜率不存在时,切线方程为 ![]() ;
;
②当切线斜率存在时,设切线方程为 ![]() ,
,
因为直线和圆相切,所以圆心 ![]() 到切线的距离
到切线的距离 ![]() ,解得
,解得 ![]() ,
,
所以切线方程为 ![]() ,即
,即 ![]() .
.
故答案为:所求切线方程为 ![]() 或
或 ![]()
(2)解:四边形 ![]() 的面积
的面积 ![]() ,
,
所以当 ![]() 最小时,四边形
最小时,四边形 ![]() 的面积
的面积 ![]() 最小.
最小.
又 ![]() 的最小值是圆心
的最小值是圆心 ![]() 到直线
到直线 ![]() 的距离,
的距离,
即 ![]() .
.
故答案为:四边形 ![]() 的面积最小值是
的面积最小值是 ![]() .
.
(3)证明:过 ![]() 三点的圆即以
三点的圆即以 ![]() 为直径的圆,
为直径的圆,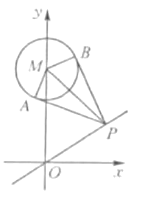
设点 ![]() ,则圆心坐标是
,则圆心坐标是 ![]() ,
,
以 ![]() 为直径的圆的方程是
为直径的圆的方程是 ![]()
![]() ,
,
化简,得 ![]() ,
,
即 ![]() .(*)
.(*)
令 ![]() ,解得
,解得 ![]() 或
或 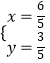 .
.
由于不论 ![]() 为何值,点
为何值,点 ![]() 、
、 ![]() 的坐标都适合方程(*),所以经过
的坐标都适合方程(*),所以经过 ![]() 三点的圆必过定点.
三点的圆必过定点.
故答案为:定点坐标是 ![]() 和
和 ![]() .
.
【解析】(1)利用圆心到直线的距离相等求切线方程,注意直线存在的情况;
(2)先将四边形的面积表示为|PM|的函数式,通过求|PM|的最值得到四边形面积的最值;
(3)将圆的方程表示为圆系方程的形式,求出圆过定点的坐标.
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: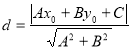 .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
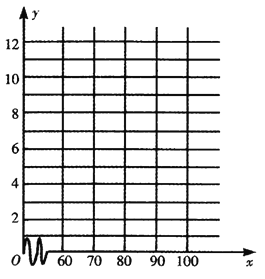
【题目】2015年一交警统计了某路段过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测在2016年该路段路况及相关安全设施等不变的情况下,车速达到110![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
(附: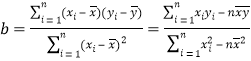 ,
,![]() ,其中
,其中![]() 为样本平均值)
为样本平均值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() …,
…,![]() …,
…,![]() ,对于
,对于![]() …,
…,![]() ,B=(
,B=(![]() …,
…,![]() ,定义A与B的差为
,定义A与B的差为
![]() …
…![]() ,A与B之间的距离为
,A与B之间的距离为![]() .
.
(Ⅰ)若![]() ,求
,求![]() ;
;
(Ⅱ)证明:对任意![]() ,有
,有
(i)![]() ,且
,且![]() ;
;
(ii)![]() 三个数中至少有一个是偶数;
三个数中至少有一个是偶数;
(Ⅲ)对于![]() …
…![]() …
…![]() ,再定义一种A与B之间的运算,并写出两条该运算满足的性质(不需证明).
,再定义一种A与B之间的运算,并写出两条该运算满足的性质(不需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx﹣
sinωx﹣ ![]() cosωx(ω<0),若y=f(x+
cosωx(ω<0),若y=f(x+ ![]() )的图象与y=f(x﹣
)的图象与y=f(x﹣ ![]() )的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣
)的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣ ![]() )的单调递增区间为( )
)的单调递增区间为( )
A.[﹣ ![]() π+
π+ ![]() ,﹣
,﹣ ![]() +
+ ![]() ](k∈Z)
](k∈Z)
B.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
C.[﹣ ![]() π+2kπ,﹣
π+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
D.[﹣ ![]() +2kπ,﹣
+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,若对任意
中,若对任意![]() 都有
都有![]() (
(![]() 为常数)成立,则称
为常数)成立,则称![]() 为“等差比数列”,下面对“等差比数列” 的判断:①
为“等差比数列”,下面对“等差比数列” 的判断:①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为
;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为![]() (其中
(其中![]() ,且
,且![]() ,
,![]() )的数列一定是等差比数列,其中正确的判断是( )
)的数列一定是等差比数列,其中正确的判断是( )
A. ①③④ B. ②③④ C. ①④ D. ①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P(x,y)(其中y ![]() )到x轴的距离比它到点F(0,1)的距离少1.
)到x轴的距离比它到点F(0,1)的距离少1.
(1)求动点P的轨迹方程;
(2)若直线l:x-y+1=0与动点P的轨迹交于A、B两点,求△OAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com