
| a+b |
| 1+a+b |
| c |
| 1+c |
| x |
| 1+x |
| x |
| 1+x |
| x1 |
| 1+x1 |
| x2 |
| 1+x2 |
| x1-x2 |
| (1+x1)(1+x2) |
| x |
| 1+x |
| a+b |
| 1+a+b |
| c |
| 1+c |


科目:高中数学 来源: 题型:
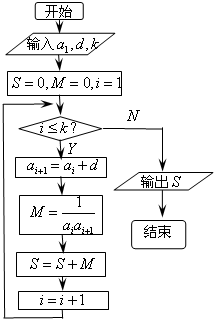 已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=
已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
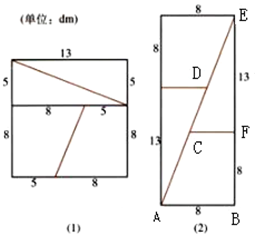 魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?
魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?查看答案和解析>>
科目:高中数学 来源: 题型:
| 3π |
| 4 |
| α |
| 2 |
| 3π |
| 8 |
| 24 |
| 25 |
| π |
| 2 |
| π |
| 2 |
| x | 0 |
|
|
π | ||||||
| y | -1 | 1 |
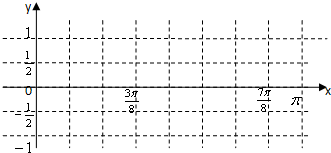
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com